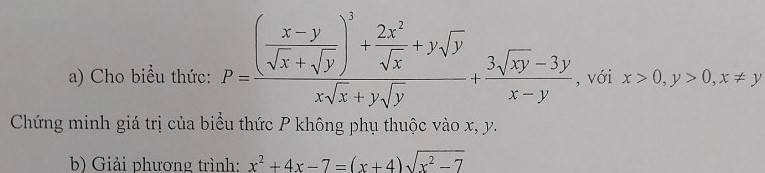\(P=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^3+2x\sqrt{x}+y\sqrt{y}}{x\sqrt{x}+y\sqrt{y}}+\dfrac{3\sqrt{y}\left(\sqrt{x}-\sqrt{y}\right)}{x-y}\)
\(=\dfrac{x\sqrt{x}-y\sqrt{y}-3x\sqrt{y}+3y\sqrt{x}+2x\sqrt{x}+y\sqrt{y}}{x\sqrt{x}+y\sqrt{y}}+\dfrac{3\sqrt{y}}{\sqrt{x}+\sqrt{y}}\)
\(=\dfrac{3x\sqrt{x}-3x\sqrt{y}+3y\sqrt{x}}{x\sqrt{x}+y\sqrt{y}}+\dfrac{3\sqrt{y}}{\sqrt{x}+\sqrt{y}}\)
\(=\dfrac{3\sqrt{x}\left(x-\sqrt{xy}+y\right)}{\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)}+\dfrac{3\sqrt{y}}{\sqrt{x}+\sqrt{y}}\)
=3
\(x^2+4x-7=\left(x+4\right)\sqrt{x^2-7}\) \(\left(ĐKXĐ:\left[{}\begin{matrix}x\ge\sqrt{7}\\x\le-\sqrt{7}\end{matrix}\right.\right)\)
\(\Leftrightarrow x^2-7-\left(x+4\right)\sqrt{x^2-7}+4x=0\)
Đặt \(\sqrt{x^2-7}=t\) \(\left(t\ge7\right)\)
\(\Rightarrow t^2-\left(x+4\right)t+4x=0\)
\(\Delta=x^2+8x+16-16x=x^2-8x+16=\left(x-4\right)^2\)
\(\left[{}\begin{matrix}t=\dfrac{x+4-x+4}{2}=4\\t=\dfrac{x+4+x-4}{2}=x\end{matrix}\right.\)
Với t=4 thì
\(\sqrt{x^2-7}=4\)
\(x^2-7=16\)
\(x=\pm\sqrt{23}\)
Với t=x thì
\(\sqrt{x^2-7}=x\)
\(x^2-7=x^2\left(vn\right)\)
Vậy.........