Question

Answer 1

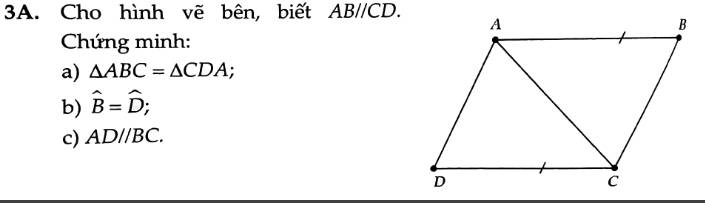
a, \(AB//CD\)

\(\Rightarrow\widehat{BAC}=\widehat{ACD}\left(soletrong\right)\)

Xét \(\Delta ABC\) và \(\Delta CDA\) có

\(AB=CD\left(gt\right)\\ \widehat{BAC}=\widehat{ACD}\left(cmt\right)\)

\(AC\) chung

\(\Rightarrow\Delta ABC=\Delta CDA\left(c-g-c\right)\)

\(b,\Rightarrow\widehat{B}=\widehat{D}\\ \Rightarrow\widehat{DAC}=\widehat{ACB}\)

\(c,\widehat{DAC}=\widehat{ACB}\left(cmt\right)\)

\(\Rightarrow AD//BC\)