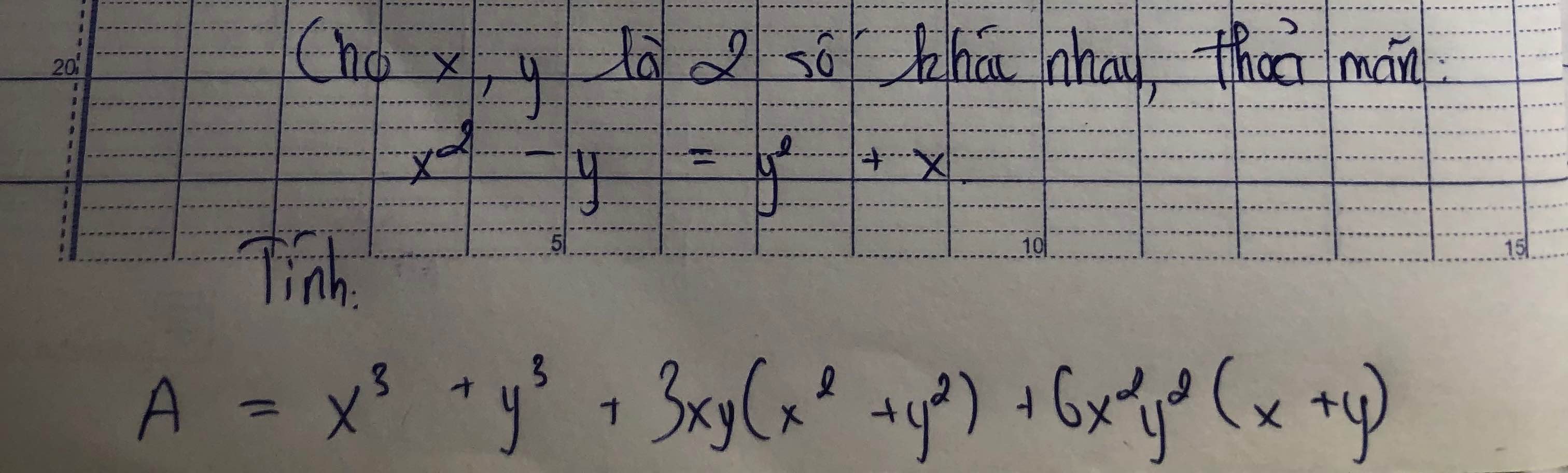Question

Answer 1

=>x^2-y^2-x-y=0

=>(x-y)(x+y)-(x+y)=0

=>(x+y)(x-y-1)=0

=>x=y+1 hoặc x=-y

TH1: x=-y

A=(-y)^3+y^3+3y*(-y)*2y^2+6(-y)^2*y^2*(-y+y)

=6y^4

TH2: x=y+1

A=(x+y)^3-3xy(x+y)+3xy[(x+y)^2-2xy]+6x^2y^2(x+y)

=(x+y)^3-3xy(x+y)+3xy(x+y)^2-6x^2y^2(x+y)+6x^2y^2(x+y)

=(x+y)^3+3xy(x+y)^3-3xy(x+y)

=(x+y)[(x+y)^2+3xy(x+y)^2-3xy]

=(2y+1)(4y^2+4y+1+3y(y+1)(4y^2+4y+1)-3y(y+1)]

=(2y+1)(4y^2+4y+1+(3y^2+3y)(4y^2+4y+1)-3y(y+1)]

=(2y+1)(4y^2+4y+1+12y^4+12y^3+12y^2+12y^3+12y^2++3y-3y^2-3y]

=(2y+1)(12y^4+24y^3+25y^2+4y+1)