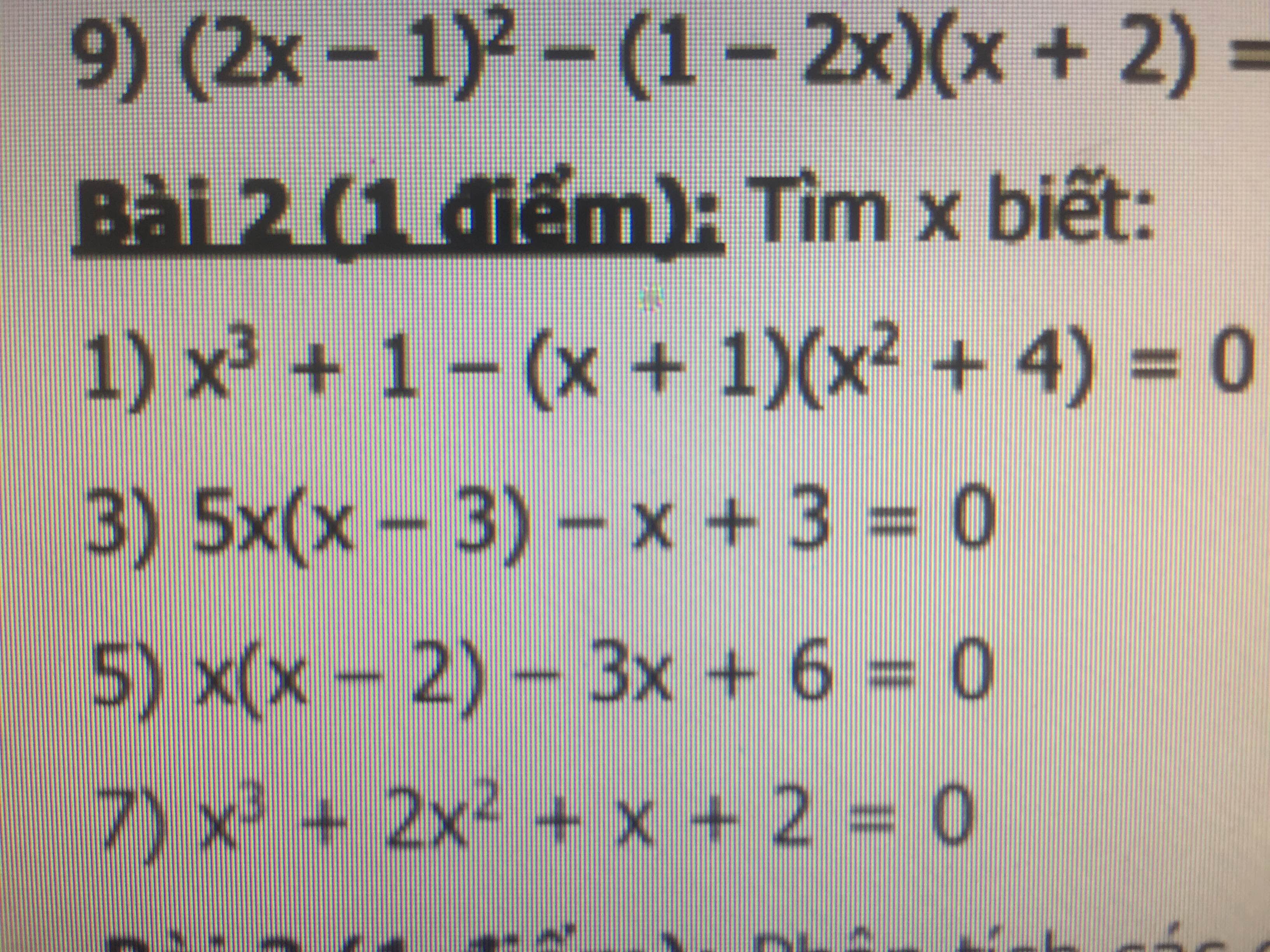1: =>(x+1)(x^2-x+1)-(x+1)(x^2+4)=0
=>(x+1)(-x-3)=0
=>x=-3 hoặc x=-1
3: \(\Leftrightarrow\left(x-3\right)\left(5x-1\right)=0\)
=>x=1/5 hoặc x=3
5: \(\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\)
=>x=2 hoặc x=3
7: =>(x+2)(x^2+1)=0
=>x=-2
1) x³ + 1 - (x + 1)(x² + 4) = 0
x³ + 1 - x³ - 4x - x² - 4 = 0
-x² - 4x - 3 = 0
-x² - x - 3x - 3 = 0
(-x² - x) + (-3x - 3) = 0
-x(x + 1) - 3(x + 1) = 0
(x + 1)(-x - 3) = 0
x + 1 = 0 hoặc -x - 3 = 0
*) x + 1 = 0
x = -1
*) -x - 3 = 0
-x = 3
x = -3
Vậy x = -3; x = -1
3) 5x(x - 3) - x + 3 = 0
5x(x - 3) - (x - 3) = 0
(x - 3)(5x - 1) = 0
x - 3 = 0 hoặc 5x - 1 = 0
*) x - 3 = 0
x = 3
*) 5x - 1 = 0
5x = 1
x = 1/5
Vậy x = 1/5; x = 3
5) x(x - 2) - 3x + 6 = 0
x(x - 2) - (3x - 6) = 0
x(x - 2) - 3(x - 2) = 0
(x - 2)(x - 3) = 0
x - 2 = 0 hoặc x - 3 = 0
*) x - 2 = 0
x = 2
*) x - 3 = 0
x = 3
Vậy x = 2; x = 3
7) x³ + 2x² + x + 2 = 0
(x³ + 2x²) + (x + 2) = 0
x²(x + 2) + (x + 2) = 0
(x + 2)(x² + 1) = 0
Do x² + 1 > 0 với mọi x thuộc R
Suy ra x + 2 = 0
x = -2
Vậy x = -2
1)
\(< =>\left(x+1\right)\left(x^2-2x+1\right)-\left(x+1\right)\left(x^2+4\right)=0< =>\left(x+1\right)\left(x^2-2x+1-x^2-4\right)=0< =>\left[{}\begin{matrix}x+1=0\\-2x-3=0\end{matrix}\right.< =>\left[{}\begin{matrix}x=-1\\x=-\dfrac{3}{2}\end{matrix}\right.\)
3)
\(< =>5x\left(x-3\right)-\left(x-3\right)=0< =>\left(x-3\right)\left(5x-1\right)=0< =>\left[{}\begin{matrix}x-3=0\\5x-1=0\end{matrix}\right.< =>\left[{}\begin{matrix}x=3\\x=\dfrac{1}{5}\end{matrix}\right.\)
5)
\(< =>x\left(x-2\right)-3\left(x-2\right)=0< =>\left(x-2\right)\left(x-3\right)=0< =>\left[{}\begin{matrix}x-2=0\\x-3=0\end{matrix}\right.< =>\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
7)
\(< =>\left(x^3+x\right)+\left(2x^2+2\right)=0< =>x\left(x^2+1\right)+2\left(x^2+1\right)=0< =>\left(x+1\right)\left(x^2+1\right)=0< =>\left[{}\begin{matrix}x+1=0\\x^2+1=0\end{matrix}\right.< =>}x=-1\)