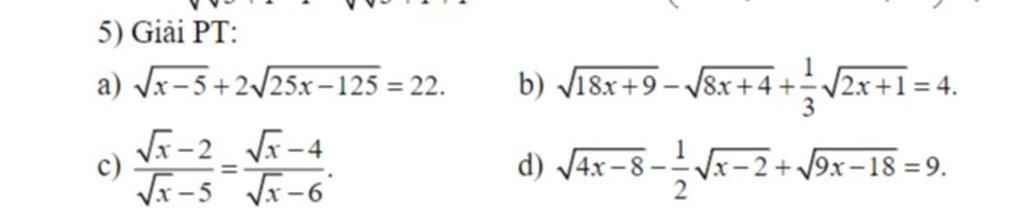\(a)\)\(\sqrt{x-5}+2\sqrt{25x-125}=22\left(ĐK:x>=5\right)\\ < =>\sqrt{x-5}+2.\sqrt{25}.\sqrt{x-5}=22\\ < =>\sqrt{x-5}.\left(1+2\sqrt{25}\right)=22\\ < =>\sqrt{x-5}.11=22\\ < =>\sqrt{x-5}=2\\ < =>x-5=4\\ < =>x=9\left(TMDK\right)=>S=\left\{9\right\}\)
\(b)\)\(\sqrt{18x+9}-\sqrt{8x+4}+\dfrac{1}{3}\sqrt{2x+1}=4\left(ĐK:x>=-\dfrac{1}{2}\right)\\ < =>\sqrt{9}.\sqrt{2x+1}-\sqrt{4}.\sqrt{2x+1}+\dfrac{1}{3}\sqrt{2x+1}=4\\ < =>\sqrt{2x+1}.\left(\sqrt{9}-\sqrt{4}+\dfrac{1}{3}\right)=4\\ < =>\sqrt{2x+1}.\dfrac{4}{3}=4\\ < =>\sqrt{2x+1}=3\\ < =>2x+1=9\\ < =>x=4\left(TMDK\right)=>S=\left\{4\right\}\)
a: \(\Leftrightarrow\sqrt{x-5}+10\sqrt{x-5}=22\)
\(\Leftrightarrow11\sqrt{x-5}=22\)
=>x-5=4
hay x=9
b: \(\Leftrightarrow3\sqrt{2x+1}-2\sqrt{2x+1}+\dfrac{1}{3}\sqrt{2x+1}=4\)
\(\Leftrightarrow\sqrt{2x+1}\cdot\dfrac{4}{3}=4\)
\(\Leftrightarrow2x+1=9\)
hay x=4
c: \(\Leftrightarrow x-8\sqrt{x}+12=x-9\sqrt{x}+20\)
\(\Leftrightarrow\sqrt{x}=8\)
hay x=64
d: \(\Leftrightarrow2\sqrt{x-2}-\dfrac{1}{2}\sqrt{x-2}+3\sqrt{x-2}=9\)
\(\Leftrightarrow4.5\cdot\sqrt{x-2}=9\)
=>x-2=4
hay x=6
\(c)\)\(\dfrac{\sqrt{x}-2}{\sqrt{x}-5}=\dfrac{\sqrt{x}-4}{\sqrt{x}-6}\left(ĐK:x>=0;x\ne\left\{25;36\right\}\right)\\ < =>\left(\sqrt{x}-2\right)\left(\sqrt{x}-6\right)=\left(\sqrt{x}-5\right)\left(\sqrt{x}-4\right)\\ < =>x-8\sqrt{x}+12=x-9\sqrt{x}+20\\ < =>x-x+9\sqrt{x}-8\sqrt{x}=20-12\\ < =>\sqrt{x}=8\\ < =>x=64\left(TMDK\right)=>S=\left\{64\right\}\)
\(d)\)\(\sqrt{4x-8}-\dfrac{1}{2}\sqrt{x-2}+\sqrt{9x-18}=9\left(ĐK:x>=2\right)\\ < =>\sqrt{4}.\sqrt{x-2}-\dfrac{1}{2}\sqrt{x-2}+\sqrt{9}.\sqrt{x-2}=9\\ < =>\sqrt{x-2}.\left(\sqrt{4}-\dfrac{1}{2}+\sqrt{9}\right)=9\\ < =>\sqrt{x-2}.\dfrac{9}{2}=9\\ < =>\sqrt{x-2}=2\\ < =>x-2=4\\ < =>x=6\left(TMDK\right)=>S=\left\{6\right\}\)
\(a.\sqrt{x-5}+2\sqrt{25x-125}=22\)
\(11\sqrt{-5+x=22}\)
\(\sqrt{-5+x}=22:11\)
\(\sqrt{-5+x}=2\)
\(-5+x=4\)
\(x=9\)
\(Vậy...\)
\(b.\sqrt{18x+9}-\sqrt{8x+4}+\dfrac{1}{3}\sqrt{2x+1}=4\)
\(4\sqrt{1+2x}=12\)
\(\sqrt{1+2x}=12:4\)
\(\sqrt{1+2x}=3\)
\(1+2x=9\)
\(x=4.\)
\(Vậy...\)
\(c.\dfrac{\sqrt{x}-2}{\sqrt{x}-5}=\dfrac{\sqrt{x}-4}{\sqrt{x}-6}\)
\(\left(\sqrt{x}-2\right)\left(\sqrt{x}-6\right)=\left(\sqrt{x}-5\right)\left(\sqrt{x}-4\right)\)
\(x-8\sqrt{x}+12=x-9\sqrt{x}+20\)
\(-8\sqrt{x}=-9\sqrt{x}+8\)
\(\sqrt{x}=8\)
\(x=64.\)
\(Vậy...\)
\(d.\sqrt{4x-8}-\dfrac{1}{2}\sqrt{x-2}+\sqrt{9x-18}=9\)
\(2\sqrt{4x-8}-\sqrt{x-2}+2\sqrt{9x-18}=18\)
\(\sqrt{-2+x=2}\)
\(-2+x=4\)
\(x=6\)
\(Vậy...\)