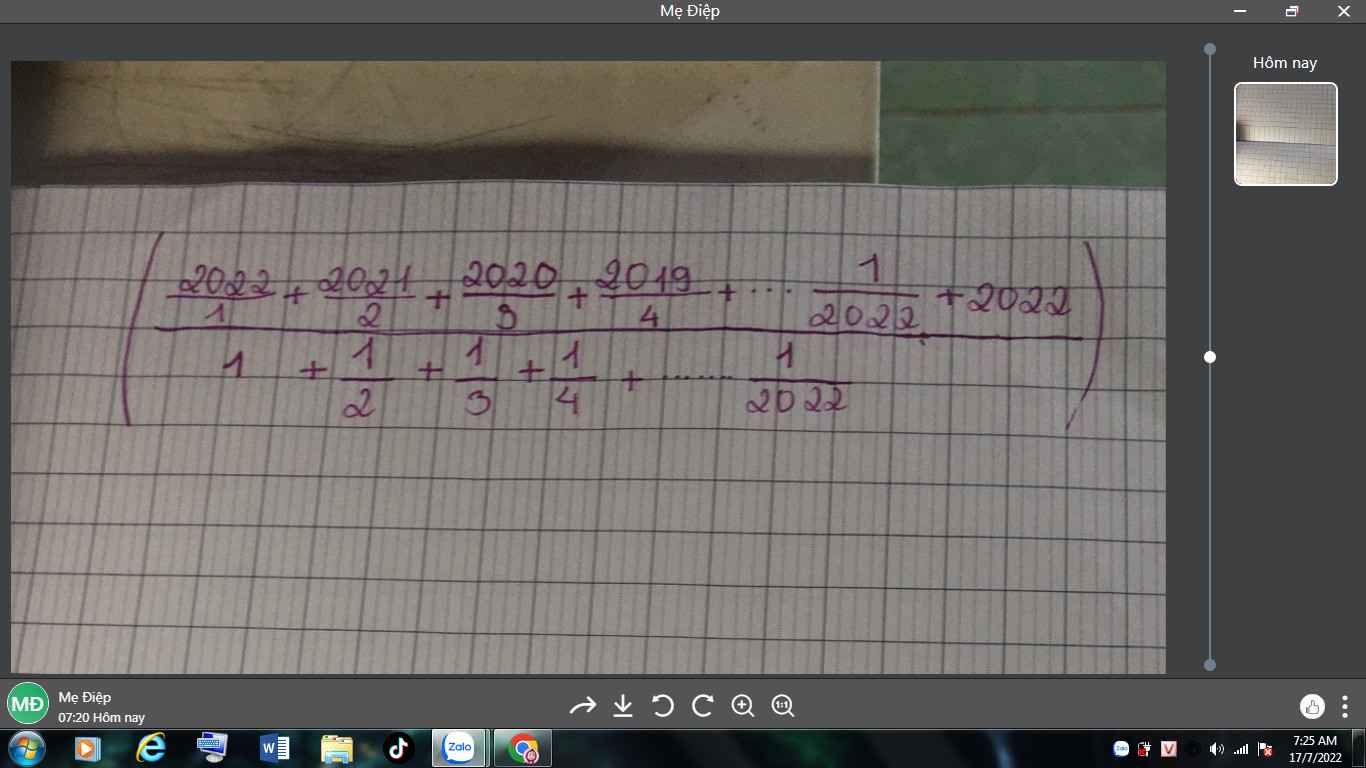
Đặt \(A=\left(\dfrac{\dfrac{2022}{1}+\dfrac{2021}{2}+...+\dfrac{2}{2021}+\dfrac{1}{2022}+2022}{1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2022}}\right)\)
\(\Rightarrow A=\dfrac{\left(\dfrac{2022}{1}+1\right)+\left(\dfrac{2021}{2}+1\right)+...+\left(\dfrac{1}{2022}+1\right)}{1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2022}}\)
\(\Rightarrow A=\dfrac{\dfrac{2023}{1}+\dfrac{2023}{2}+\dfrac{2023}{3}+...+\dfrac{2023}{2022}}{1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2022}}\)
\(\Rightarrow A=\dfrac{2023}{1}\left(\dfrac{1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2022}}{1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2022}}\right)\)
\(\Rightarrow A=2023\)
Đúng 3
Bình luận (0)