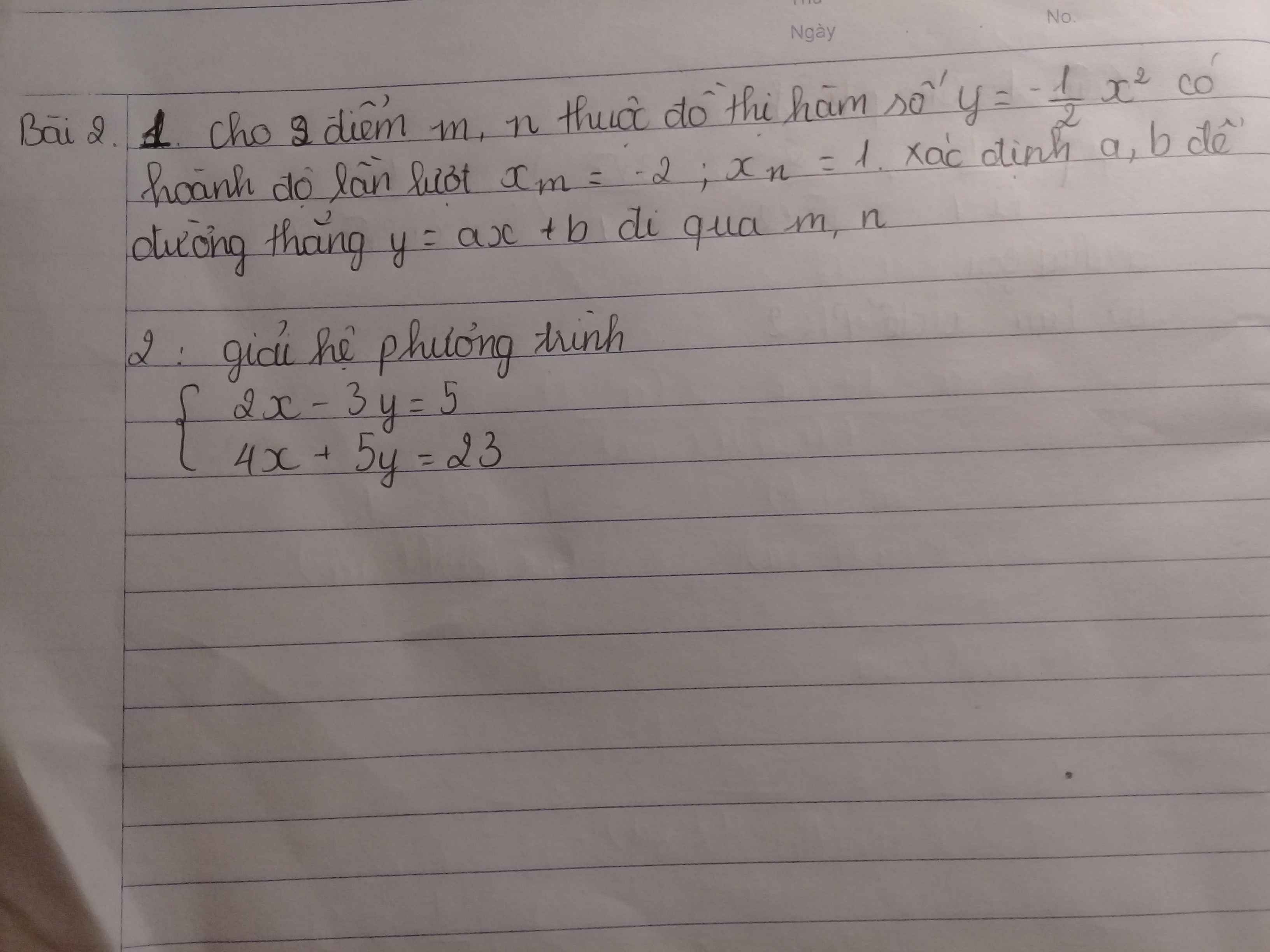Câu2:
\(\left\{{}\begin{matrix}2x-3y=5\\4x+5y=23\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x-6y=10\\4x+5y=23\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-11y=-13\\2x-3y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{13}{11}\\2x=5+3y=5+\dfrac{39}{11}=\dfrac{84}{11}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{42}{11}\\y=\dfrac{13}{11}\end{matrix}\right.\)
Câu 1:
Vì m và n ∈ \(y=\dfrac{-1}{2}x^2\)
⇒ ym = \(\dfrac{-1}{2}.\left(-2\right)^2=-2\Rightarrow M\left(-2;-2\right)\)
⇒ yn = \(\dfrac{-1}{2}.1^2=\dfrac{-1}{2}\Rightarrow N\left(1;\dfrac{-1}{2}\right)\)
Mà m và n ∈ (d) nên ta có:
\(\left\{{}\begin{matrix}-2a+b=-2\\a+b=\dfrac{-1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=-1\end{matrix}\right.\)
Vậy \(a=\dfrac{1}{2}\) và \(b=-1\)
Câu 2:
\(\left\{{}\begin{matrix}2x-3y=5\\4x+5y=23\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}4x-6y=10\\4x+5y=23\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}11y=13\\2x-3y=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{13}{11}\\x=\dfrac{47}{11}\end{matrix}\right.\)
Vậy hệ phương trình có nghiệm duy nhất \(\left(x;y\right)=\left(\dfrac{47}{11};\dfrac{13}{11}\right)\)
1.
Ta có : \(x_m=-2\Rightarrow y_m=\dfrac{1}{2}.\left(-2\right)^2=2\Rightarrow M\left(-2;2\right)\\ x_n=1\Rightarrow y_n=\dfrac{1}{2}.1^2=\dfrac{1}{2}\Rightarrow N\left(1;\dfrac{1}{2}\right)\)
Để đường thẳng y = ax + b đi qua \(M\left(-2;2\right)\) thì :
\(\Rightarrow x=-2;y=2\)
thay vào đường thẳng y = ax + b ta được : \(2=a\left(-2\right)+b\) (1)
Để đường thẳng y = ax + b đi qua \(N\left(1;\dfrac{1}{2}\right)\) thì :
\(\Rightarrow x=1;y=\dfrac{1}{2}\)
thay vào đường thẳng y = ax + b ta được : \(\dfrac{1}{2}=a.1+b\) (2)
Từ (1) và (2) ta có hệ phương trình :
\(\)\(\left\{{}\begin{matrix}-2a+b=2\\a+b=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2a+b=2\\2a+2b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2a+b=2\\3b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2a=1\\b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{1}{2}\\b=1\end{matrix}\right.\)
Vậy với \(a=-\dfrac{1}{2};b=1\) thì đường thẳng y = ax + b đi qua M , N
2.hệ abnj tự giải nhé ( do lỗi máy :))