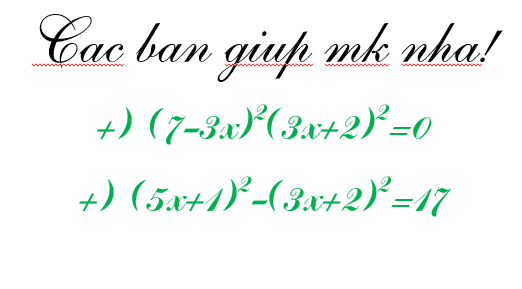a: \(\left(7-3x\right)^2\cdot\left(3x+2\right)^2=0\)
=>7-3x=0 hoặc 3x+2=0
=>x=7/3 hoặc x=-2/3
b: \(\left(5x+1\right)^2-\left(3x+2\right)^2=17\)
\(\Leftrightarrow25x^2+10x+1-9x^2-12x-4-17=0\)
\(\Leftrightarrow16x^2-2x-20=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot16\cdot\left(-20\right)=1284>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{2-2\sqrt{321}}{32}=\dfrac{1-\sqrt{321}}{16}\\x_2=\dfrac{1+\sqrt{321}}{16}\end{matrix}\right.\)
Đúng 3
Bình luận (2)
