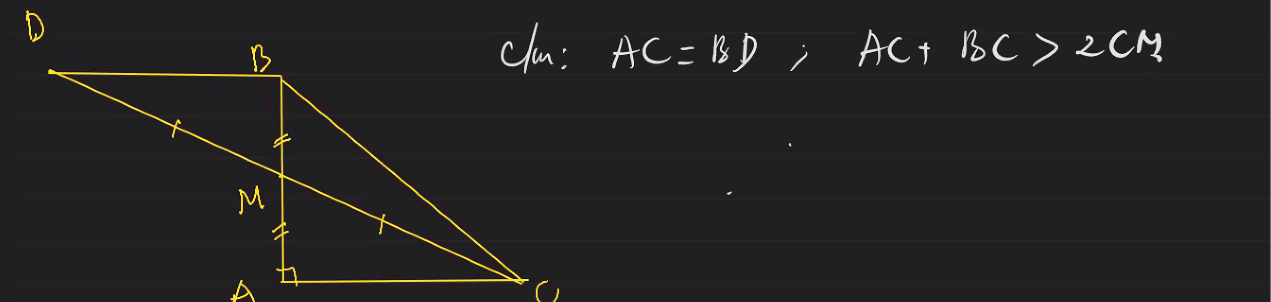Xét Δ MBD và Δ MAC
Ta có : MB = MA (gt)
MD = MC (gt)
góc BMD = góc AMC (đối đỉnh)
=> Δ MBD = Δ MAC (c.g.c)
=>AC = BD
Xét Δ MBD và Δ MAC
Ta có : MB = MA (gt)
MD = MC (gt)
góc BMD = góc AMC (đối đỉnh)
=> Δ MBD = Δ MAC (c.g.c)
=>AC = BD (2 cạnh tương ứng)
AC + BC = BD + BC > CD (bđt tam giác)
mà CD= CM+DM (2CM)
=> AC + BC > 2CM
\(\text{Xét }\Delta MBD\text{ và }\Delta MAC\text{ có:}\)
\(BM=MA\left(gt\right)\)
\(DM=MC\left(gt\right)\)
\(\widehat{DMB}=\widehat{CMA}\left(\text{đối đỉnh}\right)\)
\(\Rightarrow\Delta MBD=\Delta MAC\left(c-g-c\right)\)
\(\Rightarrow AC=BD\left(\text{hai cạnh tương ứng}\right)\)
\(\text{Ta có:MC=MD(gt)}\)
\(\Rightarrow2CM=DC\)
\(\text{Vì AC=BD(cmt)}\)
\(\Rightarrow BD+BC>DC\left(BĐT\text{ tam giác}\right)\)
\(\Rightarrow AC+BC>2CM\)