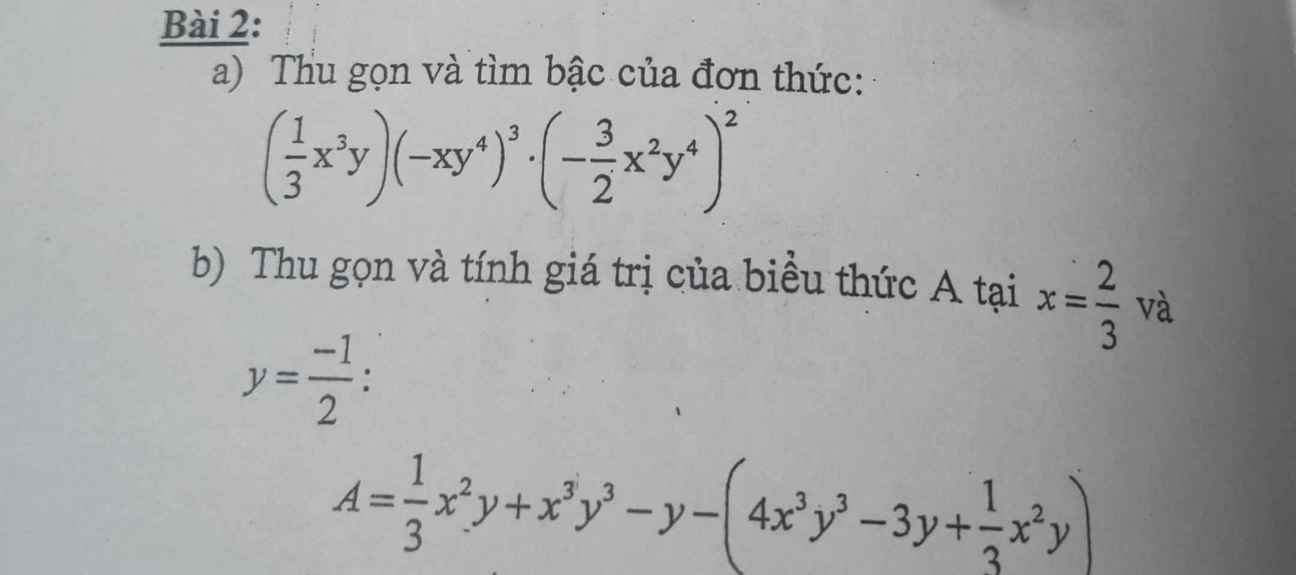Question

Answer 1

a) 

\(\left(\dfrac{1}{3}x^3y\right)\left(-xy^4\right)^3\left(-\dfrac{3}{2}x^2y^4\right)^2=\left(\dfrac{1}{3}x^3y\right)\left(-x^3y^{12}\right)\left(\dfrac{9}{4}x^4y^8\right)=\left(\dfrac{1}{3}\cdot\left(-1\right)\cdot\dfrac{9}{4}\right)\left(x^3\cdot x^3\cdot x^4\right)\left(y\cdot y^{12}\cdot y^8\right)=-\dfrac{3}{4}x^{10}y^{21}\)

Answer 2

Đơn thức trên có bậc là :10+21=31 

Answer 3

b)\(A=\dfrac{1}{3}x^2y+x^3y^3-y-\left(4x^3y^3-3y+\dfrac{1}{3}x^2y\right)=\dfrac{1}{3}x^2y+x^3y^3-y-4x^3y^3+3y-\dfrac{1}{3}x^2y=-3x^3y^3+2y\)Thay x=2/3 ; y=-1/2 vào A ta có:

\(A=-3\cdot\left(\dfrac{2}{3}\cdot\dfrac{-1}{2}\right)^3+2\cdot\dfrac{-1}{2}=-3\cdot\left(-\dfrac{1}{3}\right)^3-1=-\dfrac{3}{-27}-1=\dfrac{1}{9}-1=-\dfrac{8}{9}\)