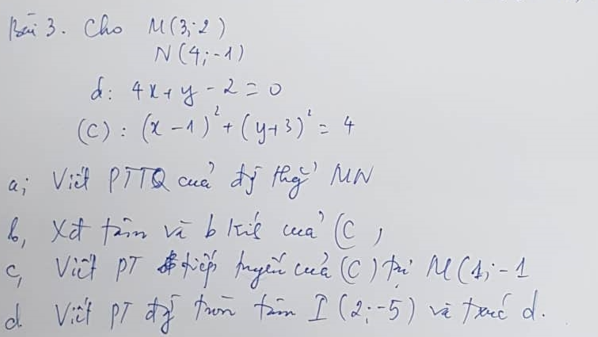a.
\(\overrightarrow{MN}=\left(1;-3\right)\Rightarrow\) đường thẳng MN nhận (3;1) là 1 vtpt
Phương trình MN:
\(3\left(x-3\right)+1\left(y-2\right)=0\Leftrightarrow3x+y-11=0\)
b.
Đường tròn (C) có tâm \(J\left(1;-3\right)\) bán kính \(R=2\)
c.
\(\overrightarrow{JM}=\left(0;2\right)=2\left(0;1\right)\)
Tiếp tuyến d tại M vuông góc JM nên nhận (0;1) là 1 vtpt
Phương trình tiếp tuyến:
\(0\left(x-1\right)+1\left(y+1\right)=0\Leftrightarrow y+1=0\)
d.
Do đường tròn tiếp xúc d nên có bán kính R thỏa mãn:
\(R=d\left(I;d\right)=\dfrac{\left|4.2-5-2\right|}{\sqrt{4^2+1^2}}=\dfrac{1}{\sqrt{17}}\)
Phương trình đường tròn:
\(\left(x-2\right)^2+\left(y+5\right)^2=\dfrac{1}{17}\)
Đúng 1
Bình luận (0)
