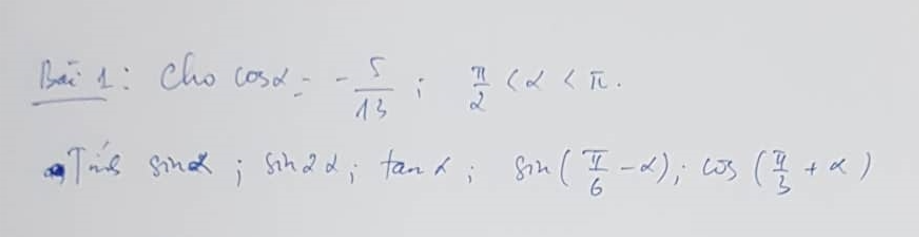\(\dfrac{\pi}{2}< a< \pi\Rightarrow sina>0\)
\(\Rightarrow sina=\sqrt{1-cos^2a}=\dfrac{12}{13}\)
\(sin2a=2sina.cosa=2.\dfrac{12}{13}.\left(-\dfrac{5}{13}\right)=-\dfrac{120}{169}\)
\(tana=\dfrac{sina}{cosa}=-\dfrac{12}{5}\)
\(sin\left(\dfrac{\pi}{6}-a\right)=sin\left(\dfrac{\pi}{6}\right)cosa-cos\left(\dfrac{\pi}{6}\right)sina=\dfrac{1}{2}.\left(-\dfrac{5}{13}\right)-\dfrac{\sqrt{3}}{2}.\dfrac{12}{13}=-\dfrac{5+12\sqrt{3}}{26}\)
\(cos\left(\dfrac{\pi}{3}+a\right)=cos\left(\dfrac{\pi}{3}\right)cosa-sin\left(\dfrac{\pi}{3}\right)sina=\dfrac{1}{2}.\left(-\dfrac{5}{13}\right)-\dfrac{\sqrt{3}}{2}.\dfrac{12}{13}=-\dfrac{5+12\sqrt{3}}{26}\)
Hoặc là: \(cos\left(\dfrac{\pi}{3}+a\right)=cos\left[\dfrac{\pi}{2}-\left(\dfrac{\pi}{6}-a\right)\right]=sin\left(\dfrac{\pi}{6}-a\right)=-\dfrac{5+12\sqrt{3}}{26}\)
Do \(\dfrac{\pi}{2}< \alpha< \pi\Rightarrow sin\alpha>0\) . Suy ra : \(sin\alpha=\sqrt{1-cos^2\alpha}=\sqrt{1-\left(-\dfrac{5}{13}\right)^2}=\sqrt{1-\dfrac{25}{169}}=\dfrac{12}{13}\)
\(sin2\alpha=2sin\alpha cos\alpha=2.\dfrac{-5}{13}.\dfrac{12}{13}=-\dfrac{120}{169}\)
tan \(\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{12}{13}:-\dfrac{5}{13}=-\dfrac{12}{5}\)
\(sin\left(\dfrac{\pi}{6}-\alpha\right)=\dfrac{1}{2}.cos\alpha-\dfrac{\sqrt{3}}{2}.sin\alpha=\dfrac{1}{2}.\dfrac{-5}{13}-\dfrac{\sqrt{3}}{2}.\dfrac{12}{13}=-\dfrac{12\sqrt{3}+5}{26}\)
\(cos\left(\dfrac{\pi}{3}+\alpha\right)=\dfrac{1}{2}cos\alpha-\dfrac{\sqrt{3}}{2}.sin\alpha=\dfrac{-12\sqrt{3}-5}{26}\)