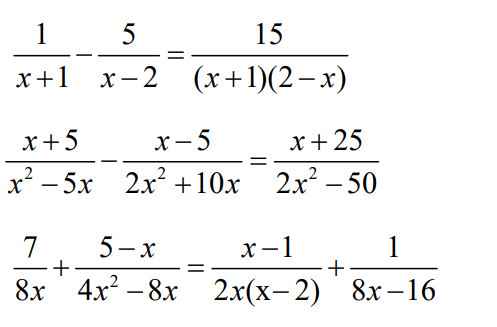a: DKXĐ: x<>-1; x<>2
PT =>\(\dfrac{x-2-5x-5}{\left(x-2\right)\left(x+1\right)}=\dfrac{-15}{\left(x+1\right)\left(x-2\right)}\)
=>-4x-7=-15
=>4x+7=15
=>x=2(loại)
b: ĐKXĐ: x<>0; x<>5; x<>-5
PT =>\(\dfrac{x+5}{x\left(x-5\right)}-\dfrac{x-5}{2x\left(x+5\right)}=\dfrac{x+25}{2\left(x-5\right)\left(x+5\right)}\)
=>\(\dfrac{2\left(x+5\right)^2-\left(x-5\right)^2}{2x\left(x+5\right)\left(x-5\right)}=\dfrac{x^2+25x}{2x\left(x+5\right)\left(x-5\right)}\)
=>2x^2+20x+50-x^2+10x-25=x^2+25x
=>x^2+30x+25=x^2+25x
=>5x=-25
=>x=-5(loại)
c: ĐKXĐ: x<>2; x<>0
PT =>\(\dfrac{7}{8x}+\dfrac{5-x}{4x\left(x-2\right)}=\dfrac{x-1}{2x\left(x-2\right)}+\dfrac{1}{8\left(x-2\right)}\)
=>\(\dfrac{7\left(x-2\right)+2\left(5-x\right)}{8x\left(x-2\right)}=\dfrac{4\left(x-1\right)+x}{8x\left(x-2\right)}\)
=>7x-14+10-2x=4x-4+x
=>3x-4=5x-4
=>x=0(loại)