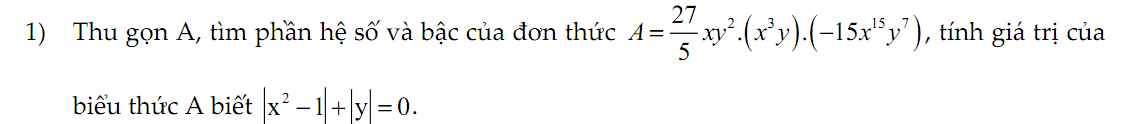\(A=\dfrac{27}{5}xy^2\left(x^3y\right)\left(-15x^{15}y^7\right)\\A=\left(\dfrac{27}{5}.\left(-15\right)\right)\left(x.x^3.x^{15}\right)\left(y^2.y.y^7\right)\\ A=-81x^{19}y^{10} \)
Hệ số của A là -81, bậc của A là \(19+10=29\).
Ta có \(\left|x^2-1\right|\ge0,\left|y\right|\ge0\)
Để \(\left|x^2-1\right|+\left|y\right|=0\) thì \(\left\{{}\begin{matrix}x^2-1=0\\y=0\end{matrix}\right.\). Khi đó \(A=0\).
Đúng 3
Bình luận (1)