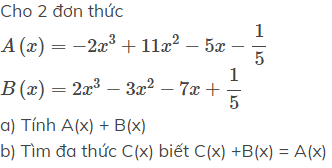Question

Answer 1

a) \(A\left(x\right)+B\left(x\right)tacó:\)

\(A+B=-2x^3+11x^2-5x-\dfrac{1}{5}+\left(2x^3-3x^2-7x+\dfrac{1}{5}\right)\)

\(A+B=-2x^3+11x^2-5x-\dfrac{1}{5}+2x^3-3x^2-7x+\dfrac{1}{5}\)

\(A+B=8x^2-12x\)

\(A+B=3x^2-4x\)

b) \(C\left(x\right)+B\left(x\right)=A\left(x\right)tacó:\)

\(C\left(x\right)=A\left(x\right)-B\left(x\right)\)

\(A\left(x\right)-B\left(x\right)=-2x^3+11x^2-5x-\dfrac{1}{5}-\left(2x^3-3x^2-7x+\dfrac{1}{5}\right)\)

\(A\left(x\right)-B\left(x\right)=-2x^3+11x^2-5x-\dfrac{1}{5}-2x^3+3x^2+7x-\dfrac{1}{5}\)

\(A\left(x\right)-B\left(x\right)=-4x^3+14x^2-2x-\dfrac{2}{5}\)

\(A\left(x\right)-B\left(x\right)=-2x^3+7x^2-x-\dfrac{1}{5}\)

Vậy C(x)+B(x)=A(x):

⇒\(C\left(x\right)=-2x^3+7x^2-x-\dfrac{1}{5}\)