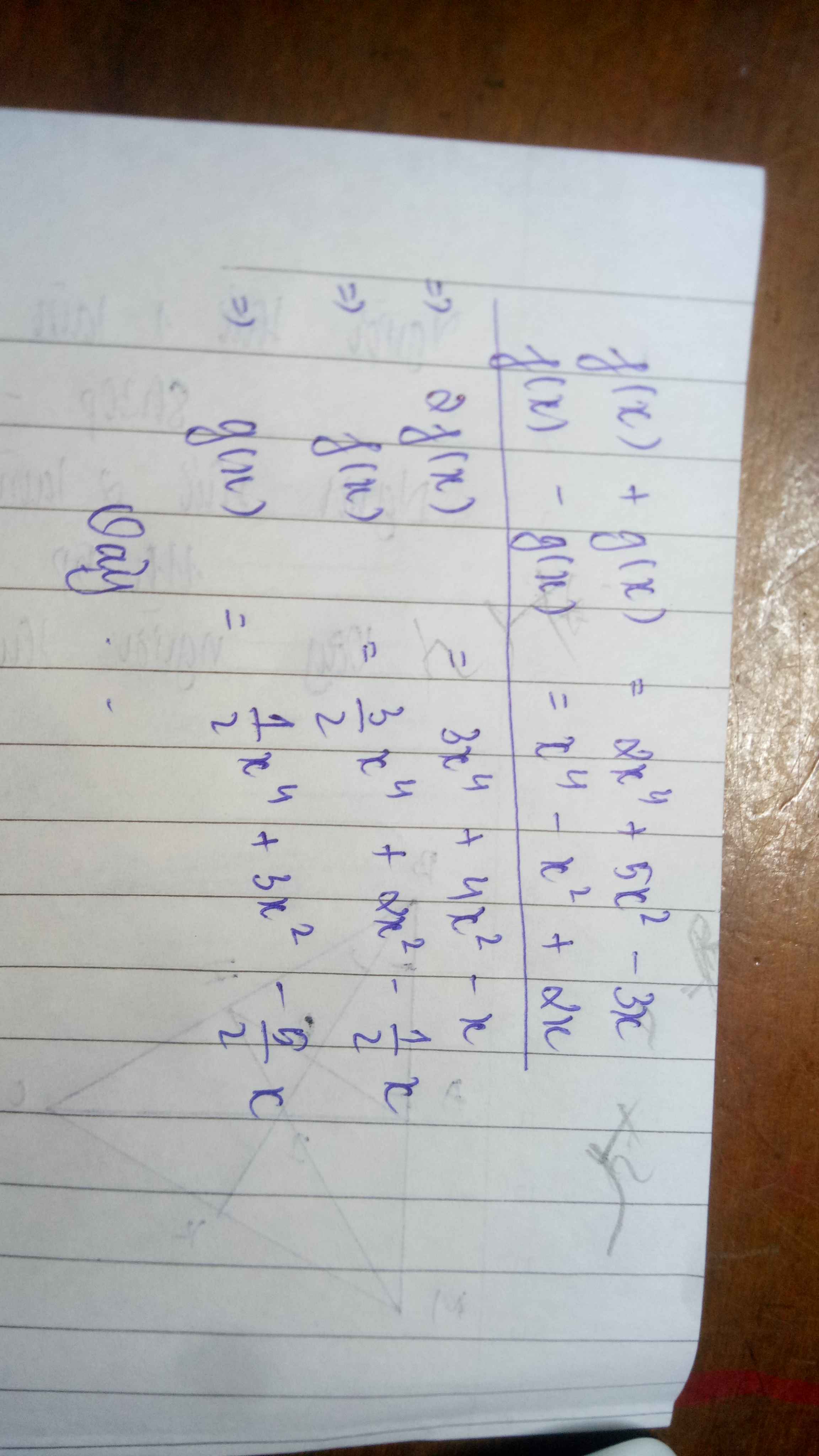
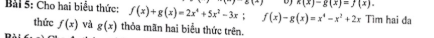Ta có:
\(f\left(x\right)+g\left(x\right)+f\left(x\right)-g\left(x\right)=2x^4+5x^2-3x+x^4-x^2+2x\\ \Rightarrow2f\left(x\right)=3x^4+4x^2-x\\ \Rightarrow f\left(x\right)=\dfrac{3x^4+4x^2-x}{2}\)
\(f\left(x\right)+g\left(x\right)-f\left(x\right)+g\left(x\right)=2x^4+5x^2-3x-x^4+x^2-2x\\ \Rightarrow2g\left(x\right)=x^4+6x^2-5x\\ \Rightarrow g\left(x\right)=\dfrac{x^4+6x^2-5x}{2}\)
Đúng 2
Bình luận (0)
