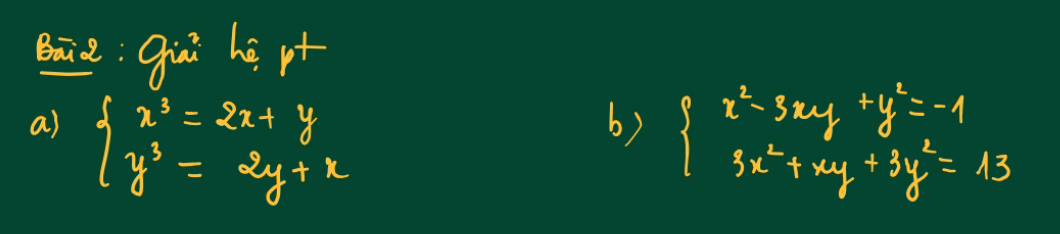a.
Lần lượt trừ vế cho vế và cộng vế với vế:
\(\left\{{}\begin{matrix}x^3-y^3=x-y\\x^3+y^3=3\left(x+y\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-y\right)\left(x^2+xy+y^2-1\right)=0\\\left(x+y\right)\left(x^2-xy+y^2-3\right)=0\end{matrix}\right.\)
TH1: \(\left\{{}\begin{matrix}x-y=0\\x+y=0\end{matrix}\right.\) \(\Rightarrow x=y=0\)
TH2: \(\left\{{}\begin{matrix}x-y=0\\x^2-xy+y^2-3=0\end{matrix}\right.\) \(\Rightarrow x=y=\pm\sqrt{3}\)
TH3: \(\left\{{}\begin{matrix}x^2+xy+y^2-1=0\\x+y=0\end{matrix}\right.\) \(\Rightarrow\left(x;y\right)=\left(1;-1\right);\left(-1;1\right)\)
TH4: \(\left\{{}\begin{matrix}x^2+xy+y^2-1=0\\x^2-xy+y^2-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+y\right)^2-xy=1\\\left(x+y\right)^2-3xy=3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left(x+y\right)^2=0\\xy=-1\end{matrix}\right.\)
\(\Rightarrow\left(x;y\right)=\left(-1;1\right);\left(1;-1\right)\)
b.
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+y\right)^2-5xy=-1\\3\left(x+y\right)^2-5xy=13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+y\right)^2=7\\xy=\dfrac{8}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+y=\sqrt{7}\\xy=\dfrac{8}{5}\end{matrix}\right.\\\left\{{}\begin{matrix}x+y=-\sqrt{7}\\xy=\dfrac{8}{5}\end{matrix}\right.\end{matrix}\right.\)
Hệ S, P cơ bản