Vẽ đồ thị hàm số y=ax^2 biết rằng đồ thị hàm số đi qua điểm A(3,9)
3.
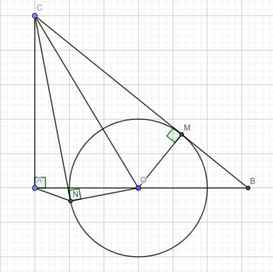
BC tiếp xúc (O) tại M \(\Rightarrow OM\perp CM\) (1)
Cx tiếp xúc (O) tại N \(\Rightarrow ON\perp CN\) (2)
Tam giác ABC vuông tại A \(\Rightarrow\) tam giác AOC vuông tại A (3)
(1);(2);(3) \(\Rightarrow\) M, N, A cùng nhìn OC dưới 1 góc vuông hay 5 điểm A, M, O, N, C cùng thuộc đường tròn đường kính OC
Hay tứ giác MONC nội tiếp
b.
Từ câu a \(\Rightarrow\widehat{AON}=\widehat{ACN}\) (cùng chắn cung AN của đường tròn đường kính OC)
4.
Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=2011^{2012}\\x_1x_2=1\end{matrix}\right.\)
\(\left\{{}\begin{matrix}y_1=x_1^2+1\\y_2=x_2^2+1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}y_1+y_2=x_1^2+x_2^2+2\\y_1y_2=x_1^2x_2^2+x_1^2+x_2^2+1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y_1+y_2=\left(x_1+x_2\right)^2-2x_1x_2+2\\y_1y_2=\left(x_1x_2\right)^2+\left(x_1+x_2\right)^2-2x_1x_2+1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y_1+y_2=2011^{4024}-2.1+2\\y_1y_2=1^2+2011^{4024}-2.1+1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y_1+y_2=2011^{4024}\\y_1y_2=2011^{4024}\end{matrix}\right.\)
\(\Rightarrow\) Theo Viet đảo, \(y_1;y_2\) là nghiệm: \(y^2-2011^{4024}y+2011^{4024}=0\)