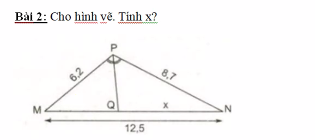
Xét ΔPMN có PQ là phân giác
nên MQ/MP=NQ/NP
=>MQ/6,2=NQ/8,7
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{MQ}{6.2}=\dfrac{NQ}{8.7}=\dfrac{MQ+ND}{6.2+8.7}=\dfrac{12.5}{14.9}=\dfrac{125}{149}\)
=>x=2175/298
Áp dụng định lý phân giác ta có:
\(\dfrac{QN}{MQ}=\dfrac{NP}{MP}\\ \Rightarrow\dfrac{NQ}{MQ}=\dfrac{8,7}{6,2}\\ \Rightarrow\dfrac{NQ}{8,7}=\dfrac{MQ}{6,2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{NQ}{8,7}=\dfrac{MQ}{6,2}=\dfrac{NQ+MQ}{8,7+6,2}=\dfrac{MN}{14,9}=\dfrac{12,5}{14,9}=\dfrac{125}{149}\)
\(\dfrac{NQ}{8,7}=\dfrac{125}{149}\Rightarrow NQ=\dfrac{2175}{298}\Rightarrow x=\dfrac{2175}{298}\)
Xét△PMN có PQ là đường phân giác; Q ∈ MN:
⇒\(\dfrac{MQ}{PM}=\dfrac{NQ}{NP}\)⇒\(\dfrac{QM}{6,2}=\dfrac{QN}{8,7}\)=\(\dfrac{QM+QN}{6,2+8,7}=\dfrac{MN}{14,9}=\dfrac{12,5}{14,9}\)(áp dụng tính chất dãy tỉ số bằng nhau)
⇒\(\dfrac{QN}{NP}=\dfrac{12,5}{14,9}=\dfrac{125}{149}\)⇒\(\dfrac{x}{8,7}=\dfrac{125}{149}\)⇒x=\(\dfrac{2175}{298}\)