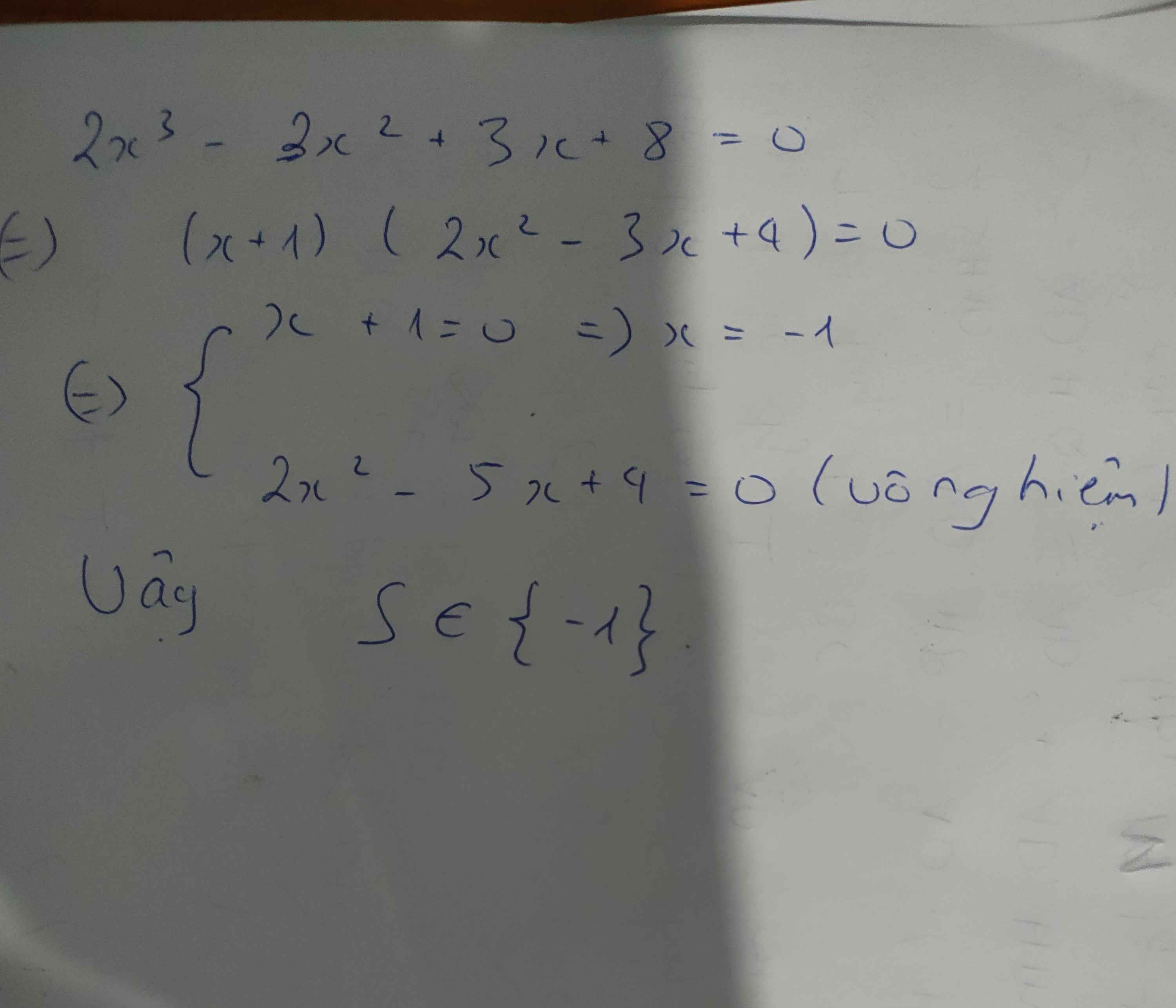\(\Rightarrow2x^2\left(x+1\right)-5x\left(x+1\right)+8\left(x+1\right)=0\)
\(\Rightarrow\left(x+1\right)\left(2x^2-5x+8\right)=0\)
\(\Rightarrow x+1=0\Rightarrow x=-1\)(do \(2x^2-5x+8=2\left(x-\dfrac{5}{4}\right)^2+\dfrac{39}{8}\ge\dfrac{39}{8}>0\))
\(PT\Leftrightarrow2x^3+2x^2-5x^2-5x+8x+8=0\)
\(\Leftrightarrow2x^2\left(x+1\right)-5x\left(x+1\right)+8\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(2x^2-5x+8\right)=0\)
Chứng minh được: \(2x^2-5x+8>0\forall x\)
\(\Rightarrow x+1=0\)
\(\Leftrightarrow x=-1\)
Vậy: \(S=\left\{-1\right\}\)
\(2x^3-3x^2+3x+8=0\\ \Leftrightarrow\left(2x^3+2x^2\right)-\left(5x^2+5x\right)+\left(8x+8\right)=0\\ \Leftrightarrow2x^2\left(x+1\right)-5x\left(x+1\right)+8\left(x+1\right)=0\\ \Leftrightarrow\left(2x^2-5x+8\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x^2-5x+8=0\\x=-1\end{matrix}\right.\)
Ta có: \(2x^2-5x+8=0\)
\(\Leftrightarrow16x^2-40x+48=0\\ \Leftrightarrow\left[\left(4x\right)^2-2.4x.5+5^2\right]+23=0\\ \Leftrightarrow\left(4x-5\right)^2+23=0\left(vô.lí\right)\)
Vậy pt có tập nghiệm \(S=\left\{-1\right\}\)