a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{BAD}\) chung
Do đó: ΔADB\(\sim\)ΔAEC
b: Xét ΔEHB vuông tại E và ΔDHC vuông tại D có
\(\widehat{EHB}=\widehat{DHC}\)
Do đó: ΔEHB\(\sim\)ΔDHC
Suy ra: HE/HD=HB/HC
hay HE/HB=HD/HC
Xét ΔHED và ΔHBC có
HE/HB=HD/HC
\(\widehat{EHD}=\widehat{BHC}\)
Do đó: ΔEHD\(\sim\)ΔBHC
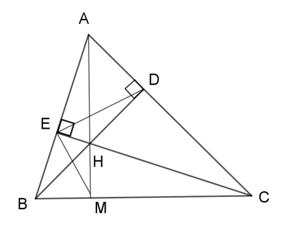
a, Xét △ADB và △AEC có:
góc ADB = góc AEC = 90\(^o\)
AD=EC ( đều là đường cao của Δ ABC)
=> ΔADB ∼ΔAEC(g-c)(đpcm)
b,
a) Xét 
và 
có:
(2 góc đối đỉnh)
(g – g)(đpcm)
c,
vẽ AM \(\perp\)BC tại M (M thuộc BC)
<=> HM \(\perp\)BC
Xét Δ BHM và ΔBCD có :
góc BEH = góc BCD= 90\(^o\)
DBC góc chung
=> Δ BHM ∼ ΔBCD (g-g)
=>\(\dfrac{BM}{BD}=\dfrac{BH}{BC}\)\(\Leftrightarrow BM.BC=BD.BH\)(1)
Xét Δ CMH và Δ CEB có :
góc BCE chung
góc HMC = góc CEB = 90\(^o\)
=> Δ CMH ∼ Δ CEB (g-g)
\(\Rightarrow\)\(\dfrac{CH}{CB}=\dfrac{CM}{CE}\Leftrightarrow CH.CE=CB.CM\)(2)
Cộng (1) và (2) , cộng vế ta được :
BD.BH+CH.CE=BM.BC+CB.CM
\(\Leftrightarrow BH.BD+CH.CE=BC.\left(BM+CM\right)\)
VÌ BM + CM =BC nên :
\(\Leftrightarrow BH.BD+CH.CE=BC.BC=BC^2\)
Vậy kết luận : \(BH.BD+CH.CE=BC^2\left(đpcm\right)\)
