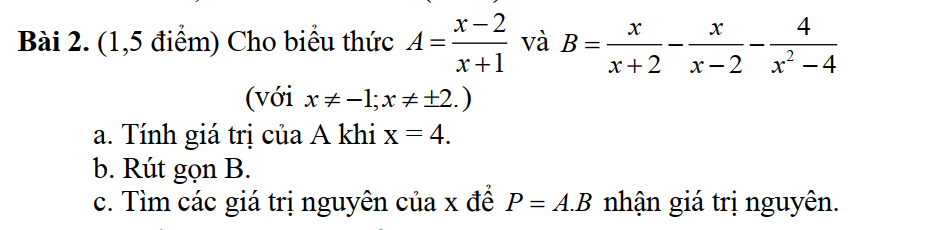Question

Answer 1

a: Thay x=4 vào A, ta được:

\(A=\dfrac{4-2}{4+1}=\dfrac{3}{5}\)

b: \(B=\dfrac{x^2-2x-x^2-2x-4}{\left(x+2\right)\left(x-2\right)}=\dfrac{-4x-4}{\left(x+2\right)\left(x-2\right)}\)

Answer 2

\(a,A=\dfrac{4-2}{4+1}=\dfrac{2}{5}\\ b,B=\dfrac{x^2-2x-x^2-2x-4}{\left(x-2\right)\left(x+2\right)}=\dfrac{-4x-4}{\left(x-2\right)\left(x+2\right)}\\ c,P=AB=\dfrac{x-2}{x+1}\cdot\dfrac{-4\left(x+1\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{-4}{x+2}\in Z\\ \Leftrightarrow x+2\inƯ\left(-4\right)=\left\{-4;-2;-1;1;2;4\right\}\\ \Leftrightarrow x\in\left\{-6;-4;-3;0\right\}\left(x\ne-1;2\right)\)