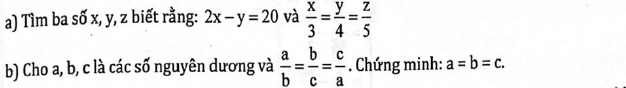Question

Answer 1

\(a,\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{2x-y}{6-4}=\dfrac{20}{2}=10\\ \Rightarrow\left\{{}\begin{matrix}x=30\\y=40\\z=50\end{matrix}\right.\\ b,\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{a}=\dfrac{a+b+c}{a+b+c}=1\\ \Rightarrow\left\{{}\begin{matrix}a=b\\b=c\\c=a\end{matrix}\right.\Rightarrow a=b=c\)

Answer 2

a) \(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)

⇒ \(\dfrac{2x}{6}=\dfrac{y}{4}=\dfrac{z}{5}\)

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\(\dfrac{2x}{6}=\dfrac{y}{4}=\dfrac{2x-y}{6-4}=\dfrac{20}{2}=10\)

⇒ \(\left\{{}\begin{matrix}x=10.3=30\\y=10.4=40\\z=10.5=50\end{matrix}\right.\)