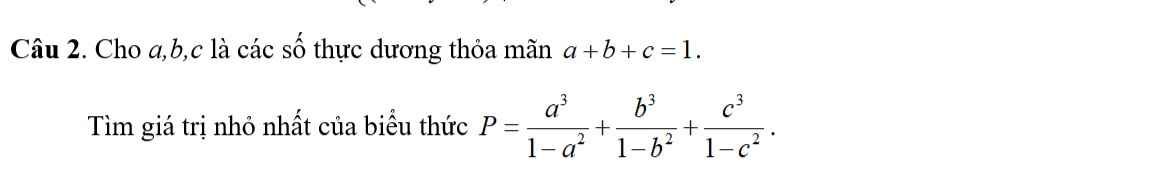Question

Answer 1

Lời giải:
\(2P=a^3(\frac{1}{1-a}+\frac{1}{1+a})+b^3(\frac{1}{1-b}+\frac{1}{1+b})+c^3(\frac{1}{1-c}+\frac{1}{c+1})\)

\(=\sum \frac{a^3}{1-a}+\sum \frac{a^3}{1+a}=\sum \frac{a^3}{b+c}+\sum \frac{a^3}{2a+b+c}\)

\(=\sum \frac{a^4}{ab+ac}+\sum \frac{a^4}{2a^2+ab+ac}\geq \frac{(a^2+b^2+c^2)^2}{2(ab+bc+ac)}+\frac{(a^2+b^2+c^2)^2}{2(a^2+b^2+c^2+ab+bc+ac)}\) (theo BĐT Cauchy-Schwarz)

\(\geq \frac{(a^2+b^2+c^2)^2}{2(a^2+b^2+c^2)}+\frac{(a^2+b^2+c^2)^2}{4(a^2+b^2+c^2)}=\frac{3}{4}(a^2+b^2+c^2)\) (theo BĐT AM-GM)

\(\geq \frac{3}{4}.\frac{1}{3}(a+b+c)^2=\frac{1}{4}\)

\(\Rightarrow P\geq \frac{1}{8}\)

Vậy $P_{\min}=\frac{1}{8}$ khi $a=b=c=\frac{1}{3}$