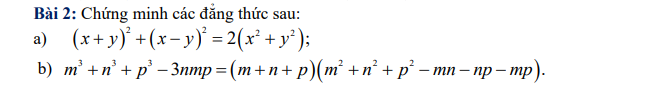Question

Answer 1

a: Ta có: \(\left(x+y\right)^2+\left(x-y\right)^2\)

\(=x^2+2xy+y^2+x^2-2xy+y^2\)

\(=2x^2+2y^2\)

\(=2\left(x^2+y^2\right)\)

Answer 2

a)\(\left(x+y\right)^2+\left(x-y\right)^2=x^2+2xy+y^2+x^2-2xy+y^2=2\left(x^2+y^2\right)\)

b)\(m^3+n^3+p^3-3mnp=\left(m+n\right)^3-3mn\left(m+n\right)+p^3-3mnp=\left(m+n+p\right)^3-3\left(m+n\right)p\left(m+n+p\right)-3mn\left(m+n+p\right)=\left(m+n+p\right)\left(m^2+n^2+p^2+2mn+2np+2mp-3mp-3np-3mn\right)=\left(m+n+p\right)\left(m^2+n^2+p^2-mn-np-mp\right)\)