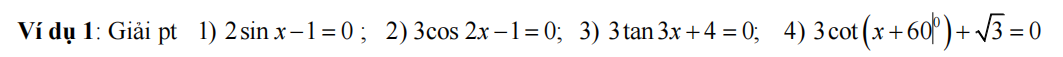\(1,\\ 2\sin x-1=0\Leftrightarrow\sin x=\dfrac{1}{2}\Leftrightarrow\sin x=\sin\dfrac{\pi}{6}\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\left(k\in Z\right)\)
\(2,\\ 3\cos2x-1=0\Leftrightarrow\cos2x=\dfrac{1}{3}\\ \Leftrightarrow2x=\pm arc\cos\dfrac{1}{3}+k2\pi\\ \Leftrightarrow x=\pm arc\cos\dfrac{1}{6}+k\pi\)
1.
\(2sinx-1=0\)
\(\Leftrightarrow sinx=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
2.
\(3cos2x-1=0\)
\(\Leftrightarrow cos2x=\dfrac{1}{3}\)
\(\Leftrightarrow2x=\pm arccos\dfrac{1}{3}+k2\pi\)
\(\Leftrightarrow x=\pm\dfrac{1}{2}arccos\dfrac{1}{3}+k\pi\)
3.
ĐK: \(x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{3}\)
\(3tan3x+4=0\)
\(\Leftrightarrow tan3x=-\dfrac{4}{3}\)
\(\Leftrightarrow3x=arctan\left(-\dfrac{4}{3}\right)+k\pi\)
\(\Leftrightarrow x=\dfrac{1}{3}arctan\left(-\dfrac{4}{3}\right)+\dfrac{k\pi}{3}\)
4.
ĐK: \(x\ne-60^o+k.180^o\)
\(3cot\left(x+60^o\right)+\sqrt{3}=0\)
\(\Leftrightarrow cot\left(x+60^o\right)=-\dfrac{\sqrt{3}}{3}\)
\(\Leftrightarrow x+60^o=-60^o+k.180^o\)
\(\Leftrightarrow x=-120^o+k.180^o\)
Đối chiếu điều kiện rồi kết luận.