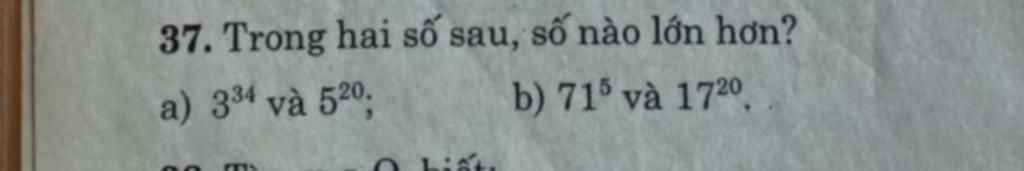Question

Answer 1

a) \(3^{34}>3^{30}=27^{10}\)

    \(5^{20}=25^{10}\)

Do \(27>25\Rightarrow27^{10}>25^{10}\)

\(\Rightarrow3^{30}>5^{20}\Rightarrow3^{34}>5^{20}\)

b) \(71^5< 72^5=\left(8.9\right)^5=8^5.9^5=8^5.3^{10}\)

    \(17^{20}>16^{20}=\left(8.2\right)^{20}=8^{20}.2^{20}=8^{20}.4^{10}\)

Do \(8^5< 8^{20},3^{10}< 4^{10}\)

\(\Rightarrow72^5< 16^{20}\)

\(\Rightarrow71^5< 17^{20}\)

Answer 2

a) \(3^{34}\) và \(5^{20}\)

Ta có: \(3^{34}>3^{30}=\left(3^3\right)^{10}=27^{10}\)

\(5^{20}=\left(5^2\right)^{10}=25^{10}\)

Vì \(27^{10}>25^{10}\) nên \(3^{34}>5^{20}\)

b) \(71^5\) và \(17^{20}\)

\(71^5< 83521^5=\left(17^4\right)^5=17^{20}\)

Vậy \(71^5< 17^{20}\)