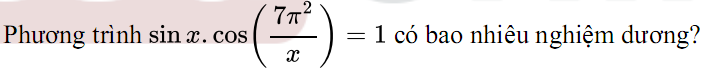\(\left\{{}\begin{matrix}sinx\le1\\cos\left(\dfrac{7\pi^2}{x}\right)\le1\end{matrix}\right.\) \(\Rightarrow sinx.cos\left(\dfrac{7\pi^2}{x}\right)\le1\)
Đẳng thức xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}sinx=1\\cos\left(\dfrac{7\pi^2}{x}\right)=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\\dfrac{7\pi^2}{x}=n2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=\dfrac{7\pi}{2n}\end{matrix}\right.\) \(\Rightarrow\dfrac{\pi}{2}+k2\pi=\dfrac{7\pi}{2n}\Rightarrow4k+1=\dfrac{7}{n}\)
\(\Rightarrow7⋮n\Rightarrow n=\left\{1;7\right\}\) (vì nghiệm dương nên n dương)
\(\Rightarrow\left[{}\begin{matrix}4k+1=7\\4k+1=1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}k=\dfrac{3}{2}\notin Z\left(loại\right)\\k=0\end{matrix}\right.\)
Phương trình có đúng 1 nghiệm dương \(x=\dfrac{\pi}{2}\)