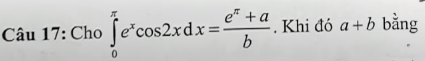Đặt \(\left\{{}\begin{matrix}u=e^x\\dv=cos2xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=e^xdx\\v=\dfrac{1}{2}sin2x\end{matrix}\right.\)
\(I=\dfrac{1}{2}e^x.sin2x|^{\pi}_0-\dfrac{1}{2}\int\limits^{\pi}_0e^xsin2xdx=-\dfrac{1}{2}\int\limits^{\pi}_0e^xsin2xdx\)
Đặt \(\left\{{}\begin{matrix}u=e^x\\dv=sin2xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=e^xdx\\v=-\dfrac{1}{2}cos2x\end{matrix}\right.\)
\(I=-\dfrac{1}{2}\left[-\dfrac{1}{2}e^xcos2x|^{\pi}_0+\dfrac{1}{2}\int\limits^{\pi}_0e^xcos2xdx\right]=-\dfrac{1}{2}\left(-\dfrac{1}{2}e^{\pi}+\dfrac{1}{2}+\dfrac{1}{2}I\right)\)
\(\Rightarrow2I=\dfrac{e^{\pi}-1}{2}-\dfrac{1}{2}I\Rightarrow I=\dfrac{e^{\pi}-1}{5}\)
\(\Rightarrow a+b=4\)