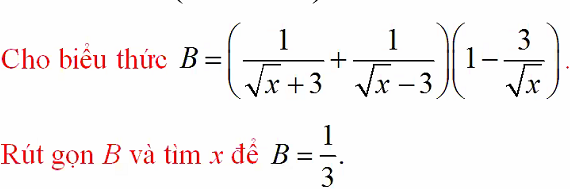ĐK: \(x>0;x\ne9\)
\(B=\left(\dfrac{1}{\sqrt{x}+3}+\dfrac{1}{\sqrt{x}-3}\right)\left(1-\dfrac{3}{\sqrt{x}}\right)\)
\(=\dfrac{\sqrt{x}-3+\sqrt{x}+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}.\dfrac{\sqrt{x}-3}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}}{\left(\sqrt{x}+3\right)\sqrt{x}}\)
\(=\dfrac{2}{\sqrt{x}+3}\)
\(B=\dfrac{1}{3}\Leftrightarrow\dfrac{2}{\sqrt{x}+3}=\dfrac{1}{3}\Leftrightarrow\sqrt{x}+3=6\Leftrightarrow x=9\left(l\right)\)
Vậy không tồn tại giá trị x để \(B=\dfrac{1}{3}\)
Ta có: \(B=\left(\dfrac{1}{\sqrt{x}+3}+\dfrac{1}{\sqrt{x}-3}\right)\cdot\left(1-\dfrac{3}{\sqrt{x}}\right)\)
\(=\dfrac{\sqrt{x}-3+\sqrt{x}+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}}\)
\(=\dfrac{2}{\sqrt{x}+3}\)
Để \(B=\dfrac{1}{3}\) thì \(\sqrt{x}+3=6\)
\(\Leftrightarrow\sqrt{x}=3\)
hay x=9(loại)