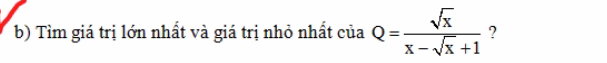Lời giải:
Áp dụng BĐT Cô-si cho hai số không âm:
$x+1\geq 2\sqrt{x}\Rightarrow x-\sqrt{x}+1\geq \sqrt{x}$
$\Rightarrow Q=\frac{\sqrt{x}}{x-\sqrt{x}+1}\leq \frac{\sqrt{x}}{\sqrt{x}}=1$
Vậy $Q_{\max}=1$. Giá trị này đạt tại $x=1$
--------------
$\sqrt{x}\geq 0$
$x-\sqrt{x}+1=(\sqrt{x}-\frac{1}{2})^2+\frac{3}{4}>0$
$\Rightarrow Q=\frac{\sqrt{x}}{x-\sqrt{x}+1}\geq 0$
Vậy $Q_{\max}=0$. Giá trị này đạt tại $x=0$
Đúng 0
Bình luận (0)