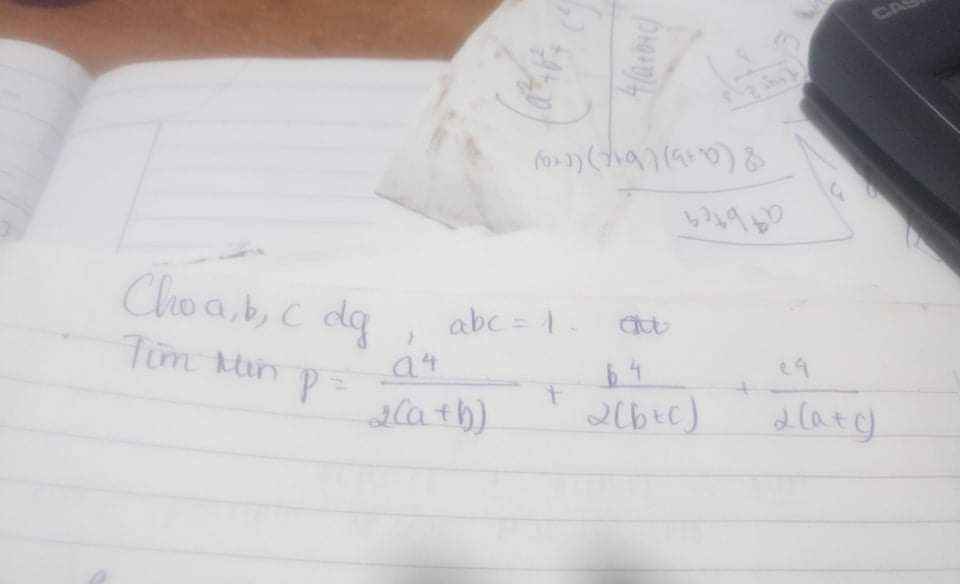Ta có:
\(\dfrac{a^4}{2\left(a+b\right)}+\dfrac{a+b}{8}+\dfrac{1}{4}+\dfrac{1}{4}\ge4\sqrt[4]{\dfrac{a^4\left(a+b\right)}{256\left(a+b\right)}}=a\)
Tương tự:
\(\dfrac{b^4}{2\left(b+c\right)}+\dfrac{b+c}{8}+\dfrac{1}{4}+\dfrac{1}{4}\ge b\)
\(\dfrac{c^4}{2\left(c+a\right)}+\dfrac{c+a}{8}+\dfrac{1}{4}+\dfrac{1}{4}\ge c\)
Cộng vế:
\(P+\dfrac{a+b+c}{4}+\dfrac{3}{2}\ge a+b+c\)
\(\Leftrightarrow P\ge\dfrac{3}{4}\left(a+b+c\right)-\dfrac{3}{2}\ge\dfrac{3}{4}.3\sqrt[3]{abc}-\dfrac{3}{2}=\dfrac{3}{4}\)
Dấu "=" xảy ra khi \(a=b=c=1\)