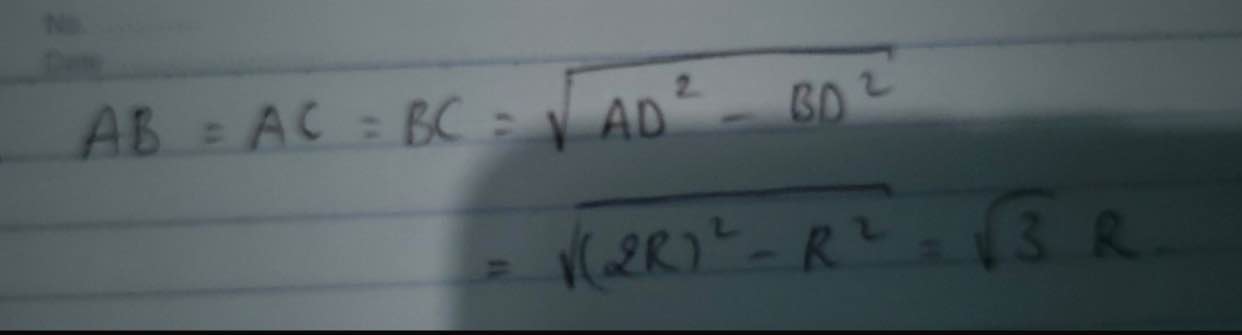a)
Xét (O) có
OI là một phần đường kính
BC là dây
OI\(\perp\)BC tại I(gt)
Do đó: I là trung điểm của dây BC(Định lí đường kính vuông góc với dây)
Xét tứ giác OBCD có
I là trung điểm của đường chéo OD(gt)
I là trung điểm của đường chéo BC(cmt)
Do đó: OBCD là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành OBCD có OB=OC(=R)
nên OBCD là hình thoi(Dấu hiệu nhận biết hình thoi)
Suy ra: OB=BD=CD=OC
Xét ΔOBD có OB=OD=BD(=R)
nên ΔOBD đều(Dấu hiệu nhận biết tam giác đều)
Suy ra: \(\widehat{OBD}=60^0\)
\(\Leftrightarrow\widehat{BOC}=180^0-60^0=120^0\)
\(\Leftrightarrow\widehat{BAC}=60^0\)
Xét ΔABC có
AI là đường cao ứng với cạnh BC(gt)
AI là đường trung tuyến ứng với cạnh BC(cmt)
\(\widehat{BAC}=60^0\)(cmt)
Do đó: ΔABC đều(Dấu hiệu nhận biết tam giác đều)



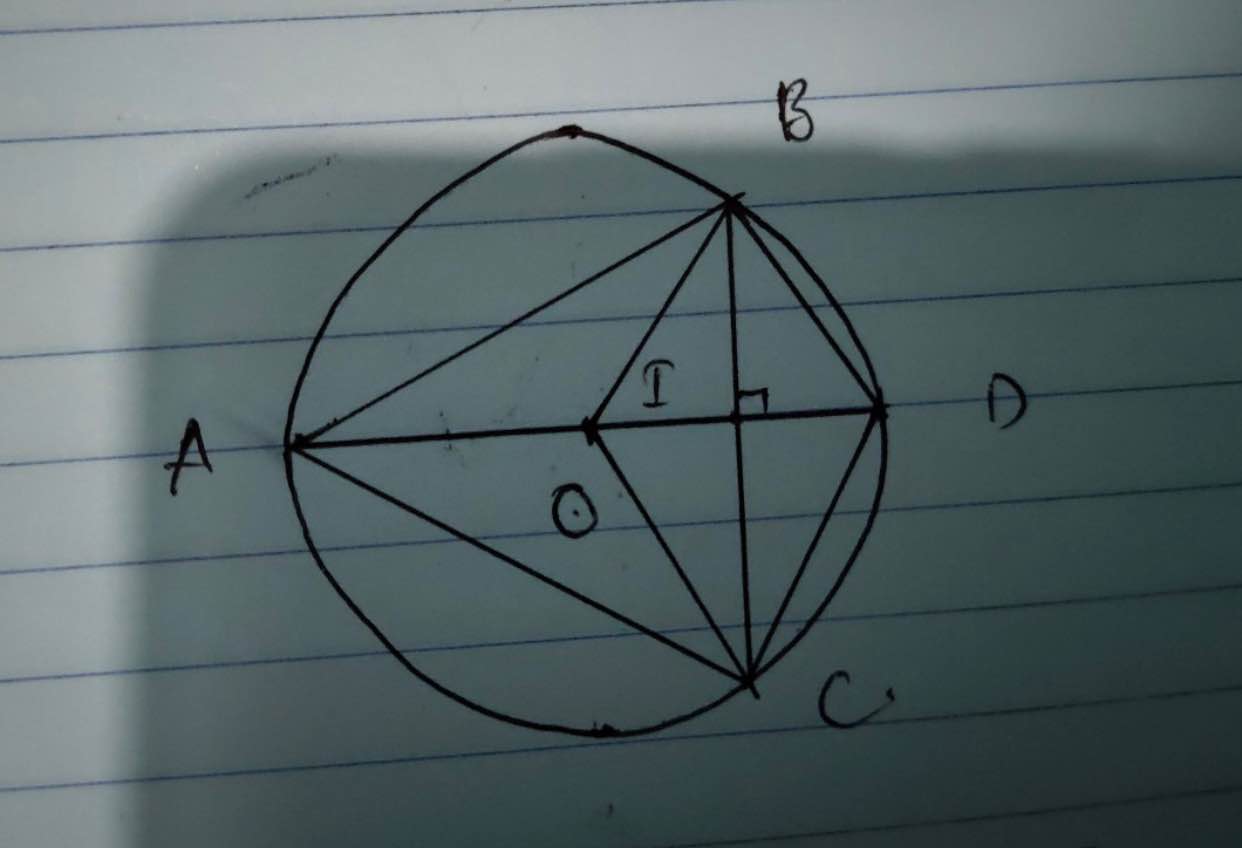 phần a)
phần a) phần b)
phần b)