Cho hàm số \(f\left(x\right)=\sqrt{x^2+3x+4}-\sqrt{-x^2+8x-15}\)
a) Tìm tập xác định A của hàm số \(f\left(x\right)\)
b) Giả sử \(B=\){ \(x\in R\)| \(4< x\le5\)}
Hãy xác định các tập A\B và R\(A\B)
Cho phương trình :
\(mx^2-2x-4m-1=0\)
a) Chứng minh rằng với mọi giá trị \(m\ne0\), phương trình đã cho có hai nghiệm phân biệt ?
b) Tìm giá trị của \(m\) để -1 là một nghiệm của phương trình. Sau đó tìm nghiệm còn lại ?
Nêu các tính chất của bất đẳng thức. Áp dụng một trong các tính chất đó, hãy so sánh các số \(2^{3000}\) và \(3^{2000}\)?
- Các tính chất của bất đẳng thức:
TC1. ( Tính chất bắc cầu)
TC2. (Quy tắc cộng)
A < B <=> A + C < B + C
TC3. (Quy tắc cộng hai bất đẳng thức dùng chiều)
TC4. (Quy tắc nhân)
TC5. (Quy tắc nhân hai bất đẳng thức)
TC6. (Quy tắc lũy thừa, khai căn)
Với A, B > 0, n ∈ N* ta có:
A < B <=> An < Bn
A < B <=> .
- Áp dụng tính chất: 0 < an < bn với n ∈ N*
Xét: 23000 = (23)1000
32000 = (32)1000
Ta có: 0<23<32 ⇒ (23)1000 < (32)1000
Do đó: 23000 < 32000
Trả lời bởi qwertyNêu cách giải thệ hai bất phương trình bậc nhất hai ẩn và giải hệ :
\(\left\{{}\begin{matrix}2x+y\ge1\\x-3y\le1\end{matrix}\right.\)
\(\left\{{}\begin{matrix}2X+Y\ge1\left(1\right)\\X-3Y\le1\left(2\right)\end{matrix}\right.\)
*Giải 2X+Y-1=0
cho đi qua 2 điểm và thử điểm O(0;0) vào (1) và loại đi phần k thỏa mãn
*Tương tự giải X-3Y-1=0
*Lấy giao (1) và (2)
Trả lời bởi Lê Văn Huya) Em hãy thu thập điểm trung bình học kì I về môn Toán của từng học sinh lớp mình ?
b) Lập bảng phân bố tần số và tần suất ghép lớp để trình bày các số liệu thống kê thu thập được theo các lớp :
[0;2); [2;4); [4;6); [6;8); [8;10]
Phát biểu định lý về dấu của một tam thức bậc hai \(f\left(x\right)=ax^2+bx+c\)
Lập bảng biến thiên và vẽ đồ thị của các hàm số :
a) \(y=-3x+2\)
b) \(y=2x^2\)
c) \(y=2x^2-3x+1\)
Y=2x²-3x+1
Trả lời bởi Nrauj HmoobHãy phát biểu các khẳng định sau đây dưới dạng điều kiện cần và đủ
Tam giác ABC vuông tại A thì \(BC^2=AB^2+AC^2\)
Tam giác ABC có các cạnh thỏa mãn hệ thức \(BC^2=AB^2+AC^2\) thì vuông tại A
Điều kiện cần và đủ của tam giác ABC vuông tại A là các cạnh của nó thỏa mãn hệ thức :
a2 + b2 = c2
(a, b, c độ dài các cạnh theo thứ tự đối diện các đỉnh A, B, C)
Phát biểu quy tắc xét dấu một nhị thức bậc nhất. Áp dụng quy tắc đó để giải bất phương trình :
\(\dfrac{\left(3x-2\right)\left(5-x\right)}{\left(2-7x\right)}\ge0\)
Quy tắc xét dấu một nhị thức dựa trên định lí :
“Nhị thức f(x) = ax + b (a≠0) có dấu cùng với hệ số a khi x lấy giá trị trong khoảng (−ba,+∞)(−ba,+∞) và trái dấu với hệ số a khi x lấy các giá trị thuộc khoảng (−∞,−ba)(−∞,−ba)”.
Áp dụng: Ta lập bảng xét dấu của vế trái f(x) của bất phương trình:
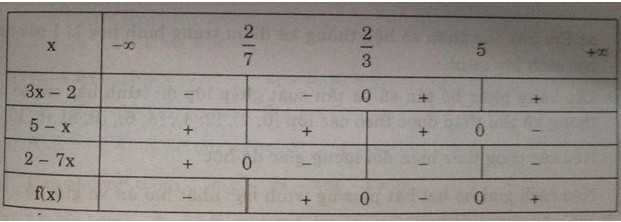
Tập nghiệm của bất phương trình: S=(27,23]∪[5,+∞)
Nêu các công thức biến đổi lượng giác đã học ?
1.Công thức cộng:
sin(x+y)=sinx.cosy+cosx.siny
sin(x-y)=sinx.cosy-cosx.siny
cos(x+y)=cosxcosy-sinxsiny
cos(x-y)=cosxcosy+sinxsiny
tan(x+y)=\(\dfrac{tanx+tany}{1-tanx.tany}\)
tan(x-y)=\(\dfrac{tanx-tany}{1+tanx.tany}\)
2.Công thức nhân đôi:
sin2x=2sinx.cosx
cos2x=cos2x-sin2x=1-2sin2x=2cos2x-1
tan2x=\(\dfrac{2tanx}{1-tan^2x}\)
3. Công thức hạ bậc:
sin2x=\(\dfrac{1-cos2x}{2}\)
cos2x=\(\dfrac{1+cos2x}{2}\)
tan2x=\(\dfrac{1-cos^2x}{1+cos^2x}\)
4. Công thức biến đổi tích thành tổng:
cosx.cosy=\(\dfrac{1}{2}\)[cos(x-y)+cos(x+y)]
sinx.siny=\(\dfrac{1}{2}\)[cos(x-y)-cos(x+y)]
sinx.cosy=\(\dfrac{1}{2}\)[sin(x-y)+sin(x+y)]
5. Công thức biến đổi tổng thành tích:
cosx+cosy=2cos\(\dfrac{x+y}{2}\).cos\(\dfrac{x-y}{2}\)
cosx-cosy=2sin\(\dfrac{x+y}{2}\).sin\(\dfrac{x-y}{2}\)
sinx+siny=2sin\(\dfrac{x+y}{2}\).cos\(\dfrac{x-y}{2}\)
sinx-siny=2cos \(\dfrac{x+y}{2}\).sin \(\dfrac{x-y}{2}\)
Trả lời bởi Mai Khanh
a) Tập xác định của f(x) :
A = {x ∈ R | x2 + 3x + 4 ≥ 0 và -x2 + 8x – 15 ≥ 0}
- x2 + 3x + 4 có biệt thức Δ = 32 – 16 < 0
Theo định lí dấu của tam thức:
x2 + 3x + 4 ≥ 0 ∀x ∈R
-x2 + 8x – 15 = 0 ⇔ x1 = 3, x2 = 5
-x2 + 8x – 15 > 0 ⇔ 3 ≤ x ≤ 5 ⇒ A = [3, 5]
b) A/B = [3, 4]
R\(A\B) = (-∞, 3) ∪ (4, +∞)
Trả lời bởi Quang Duy