Cho tam giác ABC có \(\widehat{A}\) là góc tù. Các đường trung trực của AB và của AC cắt nhau ở O và cắt BC theo thứ tự ở D và E
a) Các tam giác ABD, ACE là tam giác gì ?
b) Đường tròn tâm O bán kính OA đi qua những điểm nào trong hình vẽ ?
Cho tam giác ABC có \(\widehat{A}\) là góc tù. Các đường trung trực của AB và của AC cắt nhau ở O và cắt BC theo thứ tự ở D và E
a) Các tam giác ABD, ACE là tam giác gì ?
b) Đường tròn tâm O bán kính OA đi qua những điểm nào trong hình vẽ ?
Cho tam giác cân (không đều ) ABC có AB = AC. Hai đường trung trực của hai cạnh AB, AC cắt nhau tại O. Khi đó khẳng định nào sau đây là đúng ?
(A) OA > OB (B) \(\widehat{AOB}>\widehat{AOC}\)
(C) \(OA\perp BC\) (D) O cách đều ba cạnh của tam giác ABC
Cho tam giác ABC vuông tại A. Gọi P, Q, R lần lượt là trung điểm của ba cạnh AB, AC. BC. Gọi O là giao điểm của ba đường phân giác. Khi đó, tâm đường tròn ngoại tiếp tam giác ABC là điểm :
(A) O (B) P (C) Q (D) R
Hãy chọn phương án đúng ?
Cho tam giác ABC có \(\widehat{A}=100^0\). Các đường trung trực của AB và AC lần lượt cắt BC ở E và F. Tính \(\widehat{EAF}\) ?
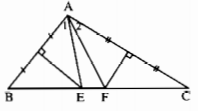
Vì E thuộc đường trung trực của đoạn thẳng AB nên EA = EB, hay tam giác EAB cân tại đỉnh E. Suy ra \(\widehat{B}=\widehat{A_1}\). Tương tự, có \(\widehat{C}=\widehat{A_2}\). Ta có:
\(\widehat{EAF}=\widehat{A}-\left(\widehat{A_1}+\widehat{A_2}\right)=\widehat{A}-\left(\widehat{B}+\widehat{C}\right)\)
Mặt khác
\(\widehat{B}+\widehat{C}=180^0-\widehat{A}=180^0-100^0=80^0\)
Trả lời bởi Đồ hút HP ngọc rồng onli...
Cho tam giác ABC có góc A là góc tù. Các đường trung trực AB; AC cắt nhau tại O và lần lượt cắt BC tại M, N. Chứng minh rằng AO là tia phân giác của góc MAN ?
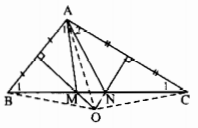
Theo bài 8.3 ta đã có\(\widehat{A_1} =\widehat{B}_1;\widehat{A_2}=\widehat{C_1} \) (1)
Ta có O là giao điểm của ba đường trung trực của tam giác ABC nên OA = OB = OC, hay các tam giác OAB, OAC, OBC cân tại O. Suy ra \(\widehat{OAB}=\widehat{OBA},\widehat{OAC}=\widehat{OCA},\widehat{OCB}=\widehat{OBC}\)Kết hợp với (1) \(\widehat{OBM}=\widehat{OAM},\widehat{OCN}=\widehat{OAN}\) hay\(\widehat{OAM}=\widehat{OBC}=\widehat{OCB}=\widehat{OAN}\) . Vậy OA là tia phân giác góc MAN.
Trả lời bởi Thảo Phương
Giải
a) D thuộc đường trung trực của AB nên DA = DB (tính chất đường trung trực)
Vậy ∆ADB cân tại D.
E thuộc đường trung trực của AC nên AE = EC (tính chất đường trung trực)
Vậy ∆AEC cân tại A.
b)Vì O là giao điểm ba đường trung trực của ∆ABC nên:
OA = OB = OC
Vậy (O;OA) đi qua ba điểm A, B, C.
Trả lời bởi Thảo Phương