Chứng minh định lí : Nếu tam giác có một đường trung tuyến đồng thời là đường trung trực ứng với cùng một cạnh thì tam giác đó là một tam giác cân
Bài 8: Tính chất ba đường trung trực của tam giác
SK
Hướng dẫn giải
Thảo luận (3)
SK
Ba gia đình quyết định đào chung một cái giếng (h.50). Phải chọn vị trí của giếng ở đây để các khoảng cách từ giếng đến các nhà bằng nhau ?

Hướng dẫn giải
Thảo luận (3)
Hướng dẫn:
Vì điểm đào giếng cách ba ngôi nhà (ba ngôi nhà không cùng nằm trên một đường thẳng) nên điểm đó chính là giao điểm ba đường trung trực của ba cạnh trong tam giác có đỉnh là ba ngôi nhà.
Trả lời bởi Thien Tu Borum
SK
Vẽ đường tròn đi qua 3 đỉnh của tam giác ABC trong các trường hợp sau
a) \(\widehat{A},\widehat{B},\widehat{C}\) đều nhọn
b) \(\widehat{A}=90^0\)
c) \(\widehat{A}>90^0\)
Hướng dẫn giải
Thảo luận (3)
Hướng dẫn:
Đường tròn đi qua ba dỉnh của tam giác gọi là đường tròn ngoại tiếp tam giác đó. Đẻ vẽ đường tròn ngoại tiếp ta cần xác định tâm của đường tròn đó. Muốn xác định tâm ta vẽ hai đường trung trực và giao điểm hai đường trung trực ( cũng là giao điểm của ba trung trực cần tìm)
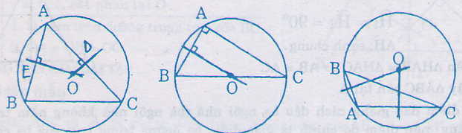
Nhận xét:
- Nếu tam giác có ba góc đều nhọn thì tâm đường tròn ngoại tiếp nằm trong tam giác.
- Nếu tam giác có góc vuông thì tâm đường tròn nằm trên cạnh huyền ( tâm là trung điểm của cạnh huyền)
- Nếu tam giác có góc tù thì tâm đường tròn ngoại tiếp nằm ngoài tam giác
Trả lời bởi Thien Tu Borum
SK
Cho hình 51 :
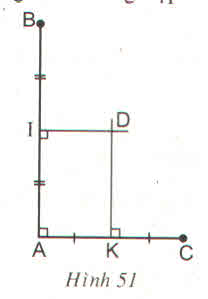
Chứng minh ba điểm B, C, D thẳng hàng
Gợi ý : Chứng minh \(\widehat{ADB}+\widehat{ADC}=180^0\)
Hướng dẫn giải
Thảo luận (2)
Hướng dẫn:
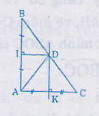
Từ hình vẽ ta có:
DK là trung trực của Ac, DI là đường trung trực của AB. Do đó ∆ADK = ∆CDK (c.c.c)
=> ˆADK=ˆCDKADK^=CDK^
hay DK là phân giác ˆADCADC^
=> ˆADKADK^ = 1212ˆADCADC^
∆ADI = ∆BDI (c.c.c)
=> ˆADI=ˆBDIADI^=BDI^
=> DI là phân giác ˆADBADB^
=> ˆADIADI^ = 1212 ˆADBADB^
Vì AC // DI ( cùng vuông góc với AB) mà DK ⊥ AC
=> DK ⊥ DI
hay ˆADKADK^ + ˆADIADI^ = 900
Do đó 1212ˆADCADC^ + 1212 ˆADBADB^ = 900
=> ˆADCADC^ + ˆADBADB^ = 1800
Trả lời bởi Thien Tu Borum
SK
Sử dụng bài 55 để chứng minh rằng : Điểm cách đều ba đỉnh của một tam giác vuông là trung điểm của cạnh huyền của tam giác đó
Từ đó hãy tính độ dài đường trung tuyến xuất phát từ đỉnh góc vuông theo độ dài cạnh huyền của một tam giác vuông ?
Hướng dẫn giải
Thảo luận (2)
a) Giả sử ∆ABC vuông góc tại A. Vẽ hai đường trung trực của hai cạnh góc vuông AB, AC cắt nhau tại M. Ta chứng minh M là trung điểm của BC.

Vì M là giao điểm hai đường trung trực d1, d2
của AB, AC mà AB ⊥ AC nên B, M, C thẳng hàng (bài tập 55)
Vì MA = MB (M thuộc đường trung trực của AB)
MA = MC (M thuộc đường trung trực của AC)
=> MB = MC
Do B, M, C thẳng hàng và M cách đều BC nên M là trung điểm của BC
b) M là trung điểm Bc => MB = 1212 BC
mà AM = MB nên MA =1212 BC
Vậy độ dài đường trung tuyến xuất phát từ đỉnh góc vuông bằng một nửa độ dài cạnh huyền.
Trả lời bởi Thien Tu Borum
SK
Có một chi tiết máy (mà đường viền ngoài là đường tròn) bị gãy (h.52)
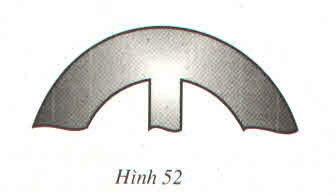
Làm thế nào để xác định được bán kính của đường viền này ?
Hướng dẫn giải
Thảo luận (2)
Lấy ba điểm phân biệt A, B, C trên đường viền ngoài, suy ra ∆ABC có đường tròn ngoại tiếp chính là đường viền ngoài. Do đó tâm đường tròn ngoại tiếp chính là giao điểm của hai đường trung trực của hai cạnh AB, AC nên ban kính là độ dài đoạn thẳng từ giao điểm O đến A
Trả lời bởi Trần Nguyễn Bảo Quyên
SK
Cho tam giác ABC. Tìm một điểm O cách đều ba điểm A, B, C ?
Hướng dẫn giải
Thảo luận (1)
điểm O cách đều ba điểm A,B,C
khi OA=OB=OC
=>O là tâm đường tròn ngoại tiếp ΔABC
Trả lời bởi Nguyễn Lê Phước Thịnh
SK
Cho hình 13.
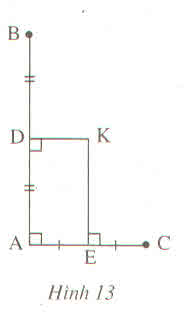
Chứng minh rằng ba điểm B, K, C thẳng hàng ?
Hướng dẫn giải
Thảo luận (1)
Nối KA,KB,KC.
Ta có KD là đường trung trực AB
=>KA=KB(tính chất đường trung trực)
\(\Rightarrow\Delta KAB\) cân tại K nên KD là đường phân giác của \(\widehat{AKB}\)
\(\Rightarrow\widehat{K_1}=\widehat{K_3}\)
\(\Rightarrow\widehat{AKB}=2\widehat{K_1}\) (1)
KE là đường trung trực của AC
=>KA=KC(tính chất đường trung trực)
\(\Rightarrow\Delta KAC\) cân tại K nên KE là đường phân giác của \(\widehat{AKC}\)
\(\Rightarrow\widehat{K_2}=\widehat{K_4}\)
\(\Rightarrow\widehat{AKC}=2\widehat{K_2}\left(2\right)\)
\(KD\perp AB\left(gt\right)\)
\(AC\perp AB\left(gt\right)\)
Trả lời bởi Hoàng Thúy An
SK
Có một chi tiết máy (mà đường viền ngoài là đường tròn) bị gẫy (h.14). Hãy nêu các xác định tâm của đường viền ?
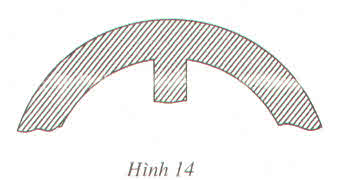
Hướng dẫn giải
Thảo luận (1)
- Lấy 3 điểm A, B, C bất kì trên đường viền. Ba điểm này tạo thành tam giác ABC và tâm và bán kính đường tròn ngoại tiếp tam giác này chính là tâm và bán kính của đường viền.
- Vẽ trung trực của 2 cạnh AB, BC, chúng cắt nhau tại O. Từ tính chất đường trung trực suy ra OA = OB = OC
Do đó O chính là tâm đường tròn này. Khi đó OA hoặc OB hoặc OC chính là bán kính cần xác định.
Trả lời bởi Angla Nguyễn
SK
Cho tam giác ABC cân tại A, đường trung tuyến AM. Đường trung trực của AC cắt đường thẳng AM ở D. Chứng minh rằng DA = DB ?
Hướng dẫn giải
Thảo luận (1)
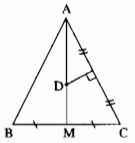
∆ABC cân tại A, AM là đường trung tuyến ứng với cạnh đáy BC nên AM cũng là đường trung trực của BC.
D là giao điểm của các đường trung trực AC và BC nên D thuộc trung trực của AB.
Vậy DA = DB (tính chất đường trung trực).
Trả lời bởi Thảo Phương
Hướng dẫn:
Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên
AH ⊥ BC và HB = HC
Xét hai tam giác vuông HAB và HAC có:
HB = HC
ˆH1=ˆH2H1^=H2^ = 900
AH: cạnh chung
Nên ∆HAB = ∆HAC => AB = AC
Vậy ∆ABC cân tại A
Trả lời bởi Thien Tu Borum