Gọi M là điểm nằm trên đường trung trực của đoạn thẳng AB. Cho đoạn thẳng MA có độ dài 5cm. Hỏi độ dài MB bằng bao nhiêu ?
Bài 7: Tính chất đường trung trực của một đoạn thẳng
SK
Hướng dẫn giải
Thảo luận (2)
SK
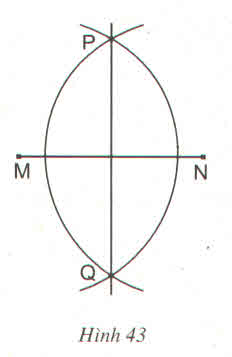
Chứng minh đường thẳng PQ được vẽ như trong hình 43 đúng là đường trung trực của đoạn thẳng MN ?
Gợi ý : Sử dụng định lí 2
Hướng dẫn giải
Thảo luận (2)
Hướng dẫn:
Ta có: Hai cung tròn tâm M và N có bán kính bằng nhau
Nên MP = NP và MQ = NQ => P; Q cách đều hai mút M, N của đoạn thẳng MN nên P; Q thuộc đường trung trực của MN hay đường thẳng qua P, Q là đường trung trực của MN
Trả lời bởi Thien Tu Borum
SK
Cho ba tam giác cân ABC, DBC, EBC có chung đáy BC. Chứng minh 3 điểm A, D, E thẳng hàng ?
Hướng dẫn giải
Thảo luận (2)
Hướng dẫn:
Vì ∆ABC cân tại A => AB = AC
=> A thuộc trung trực của BC
Vì ∆DBC cân tại D => DB = DC
=> D thuộc trung trực của BC
Vì ∆EBC cân tại E => EB = EC
=> E thuộc trung trực của BC
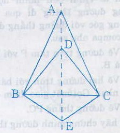
Do đó A, D, E thuộc đường trung trực của BC nên A, D, E thẳng hàng
Trả lời bởi Thien Tu Borum
SK
Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB
Chứng minh \(\Delta AMN=\Delta BMN\)
Hướng dẫn giải
Thảo luận (1)

Vì M thuộc đường trung trực của AB
=> MA = MB
N thuộc đường trung trực của AB
=> NA = NB
Do đó ∆AMN = ∆BMN (c.c.c)
SK
Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB
Chứng minh \(\Delta AMN=\Delta BMN\)
Hướng dẫn giải
Thảo luận (3)

Vì M thuộc đường trung trực của AB
=> MA = MB
N thuộc đường trung trực của AB
=> NA = NB
Do đó ∆AMN = ∆BMN (c.c.c)
SK
Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB
Chứng minh \(\Delta AMN=\Delta BMN\)
Hướng dẫn giải
Thảo luận (3)
Hướng dẫn:

Vì M thuộc đường trung trực của AB
=> MA = MB
N thuộc đường trung trực của AB
=> NA = NB
Do đó ∆AMN = ∆BMN (c.c.c)
Trả lời bởi Thien Tu Borum
SK
Hai điểm M và N cùng nằm trên một nửa mặt phẳng có bờ là đường thẳng xy. Lấy điểm L đối xứng với M qua xy. Gọi I là một điểm của xy. Hãy so sánh IM + IN với LN ?
Hướng dẫn giải
Thảo luận (3)
ướng dẫn:
Vì L và M đối xứng qua đường thẳng xy. Nên đường thẳng xy là trung trực của ML
I ∈ xt => IM = IL

Nên IM + IN = IL + IN
+ Nếu I là giao điểm của NL và xy thì IL + IN = LN
+ Nếu I không là giao điểm của NL và xy thì ba điểm I, N, L không thẳng hàng
=> IL + IN > LN
Vậy với mọi vị trí của I trên xy thì IL + IN ≥ LN
Trả lời bởi Thien Tu Borum
SK
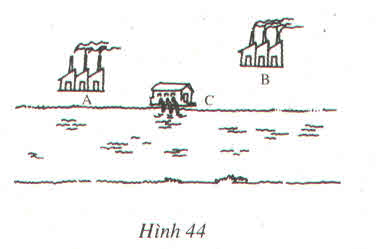
Hai nhà máy được xây dựng bên cùng một bờ sông tại hai điểm A và B (h.44). Hãy tìm trên bờ sông đó một điểm C để xây dựng trạm bơm đưa nước về cho hai nhà máy, sao cho độ dài đường ống dẫn nước là ngắn nhất ?
Hướng dẫn giải
Thảo luận (2)
Áp dụng bài 48
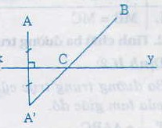
Gọi A' là điểm đối xứng của A qua đường thẳng xy chứa một bờ sông gần nhất
Ta có: CA + CB = CA' + CB ≥ A'B
Nên CA + CB ngắn nhất khi C là giao điểm của A'B với xy
Vậy điểm đặt trạm bơm là giao điểm của đường thẳng xy với đường thẳng qua điểm B và điểm A' đói xứng với A qua xy.
Trả lời bởi Tuyết Nhi Melody
SK
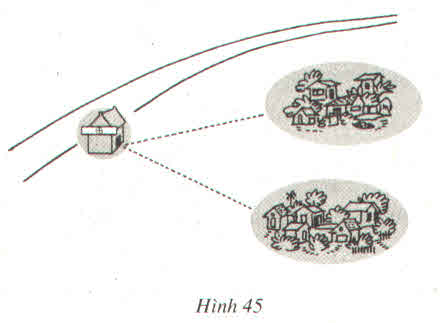
Một con đường quốc lộ cách không xa hai điểm dân cư (h.45). Hãy tìm bên đường đó một địa điểm để xây dựng một trạm y tế sao cho trạm y tế này cách đều hai điểm dân cư ?
Hướng dẫn giải
Thảo luận (3)
Gọi A và B là hai điểm dân cư, C là điểm đặt trạm y tế.

Vì C cách đều AB nên C thuộc đường trung trực của AB mà C ∈ xy nên C là giao điểm của xy và đường trung trực của AB
Trả lời bởi Trần Nguyễn Bảo Quyên
SK
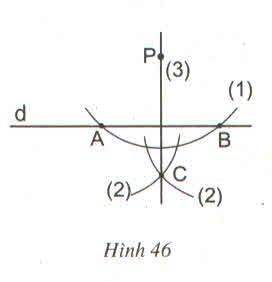
Cho đường thẳng d và điểm P không nằm trên d. Hình 46 minh họa cho cách dựng đường thẳng đi qua điểm P và vuông góc với đường thẳng d bằng thước và compa như sau :
(1) Vẽ đường tròn tâm P với bán kính thích hợp sao cho nó cắt d tại hai điểm A và B
(2) Vẽ hai đường tròn với bán kính bằng nhau có tâm tại A và B sao cho chúng cắt nhau. Gọi một giao điểm của chúng là C ( Cne P)
(3) Vẽ đường thẳng PC
Em hãy chứng minh đường thẳng PC vuông góc với d
Đố :
Tìm thêm một cách dựng nữa (bằng thước và...
Đọc tiếp
Cho đường thẳng d và điểm P không nằm trên d. Hình 46 minh họa cho cách dựng đường thẳng đi qua điểm P và vuông góc với đường thẳng d bằng thước và compa như sau :
(1) Vẽ đường tròn tâm P với bán kính thích hợp sao cho nó cắt d tại hai điểm A và B
(2) Vẽ hai đường tròn với bán kính bằng nhau có tâm tại A và B sao cho chúng cắt nhau. Gọi một giao điểm của chúng là C ( \(C\ne P\))
(3) Vẽ đường thẳng PC
Em hãy chứng minh đường thẳng PC vuông góc với d
Đố :
Tìm thêm một cách dựng nữa (bằng thước và compa)
Hướng dẫn giải
Thảo luận (3)
a) Ta có PA = PB (A, B nằm trên cung tròn có tâm P) CA = CB (hai cung tròn AB có tâm A và B có bán kính bằng nhau; C la giao điểm của 2 cung)
Vậy P; C cách đều A và B nên đường thẳng CP là đường trung trực của AB nên
PC ⊥ d
b) Một cách vẽ khác
- Lấy điểm A bất kì trên d
- Vẽ cung tròn tâm A bán kính AP cắt đường thẳng d tại M
- Vẽ cung tròn tâm M bán kính MP cắt cung tròn tâm A tại C
- Vẽ đường thẳng PC, đường thẳng PC chính là đường vuông góc với d.
=> PC ⊥ d (đpcm)
Trả lời bởi Tuyết Nhi Melody
Hướng dẫn:
Điểm M thuộc đường trung trực của AB
=> MA = MB (định lí thuận)
Vì MA = 5cm nên MB = 5cm
Trả lời bởi Thien Tu Borum