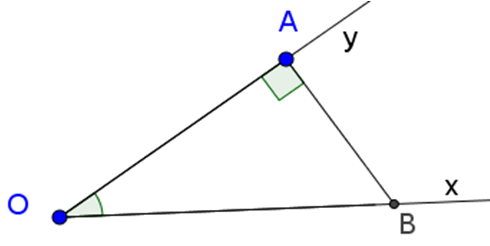
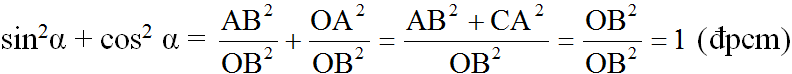Sử dụng định nghĩa các tỉ số lượng giác của một góc nhọn để chứng minh rằng : Với góc nhọn \(\alpha\) tùy ý, ta có :
a) \(tg\alpha=\dfrac{\sin\alpha}{\cos\alpha}\)
\(cotg\alpha=\dfrac{\cos\alpha}{\sin\alpha}\)
\(tg\alpha.cotg\alpha=1\)
b) \(\sin^2\alpha+\cos^2\alpha=1\)
Gợi ý : Sử dụng định lí Pytago
Hướng dẫn giải:
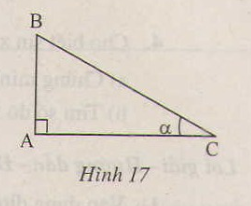
a) tgα=ABAC=AB⋅BCAC⋅BCtgα=ABAC=AB⋅BCAC⋅BC
⇒tgα=ABBC÷ACBC=sinαcosα⇒tgα=ABBC÷ACBC=sinαcosα
tgα⋅cotgα=ABAC⋅ACAB=1tgα⋅cotgα=ABAC⋅ACAB=1
cotgα=1tgα=1sinαcosα=cosαsinαcotgα=1tgα=1sinαcosα=cosαsinα
b) sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1
Nhận xét: Ba hệ thức tgα=sinαcosαtgα=sinαcosα
cotgα=cosαsinα;sin2α+cos2α=1cotgα=cosαsinα;sin2α+cos2α=1 là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khá
a) tgα=ABAC=AB⋅BCAC⋅BCtgα=ABAC=AB⋅BCAC⋅BC
⇒tgα=ABBC÷ACBC=sinαcosα⇒tgα=ABBC÷ACBC=sinαcosα
tgα⋅cotgα=ABAC⋅ACAB=1tgα⋅cotgα=ABAC⋅ACAB=1
cotgα=1tgα=1sinαcosα=cosαsinαcotgα=1tgα=1sinαcosα=cosαsinα
b) sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1
Nhận xét: Ba hệ thức tgα=sinαcosαtgα=sinαcosα
cotgα=cosαsinα;sin2α+cos2α=1cotgα=cosαsinα;sin2α+cos2α=1 là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khác.
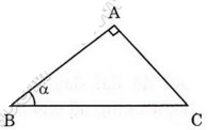
Xét tam giác ABC vuông tại A, có góc B = α
a) 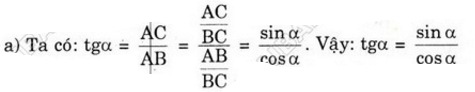
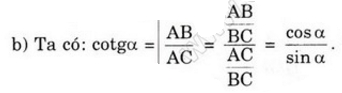
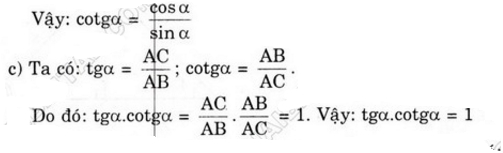
d) Tam giác ABC vuông tại A nên theo định lý pytago có:
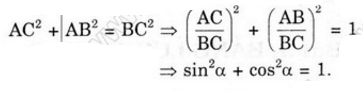
Vậy: sin²a + cos²a = 1