Tính thể tích hình chóp tam giác đều có cạnh đáy 6cm, cạnh bên \(\sqrt{15}\) cm?
\(9cm^3\).\(9\sqrt{3}cm^3\).\(\dfrac{27}{2}cm^3\).\(\dfrac{9\sqrt{3}}{2}cm^3\).Hướng dẫn giải: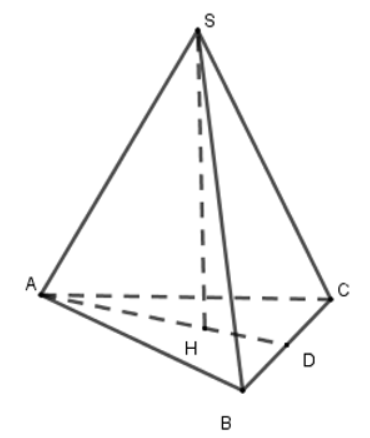
Xét chóp tam giác đều S.ABC có cạnh đáy AB=BC=CA=6cm, cạnh bên SA=SB=SC=\(\sqrt{15}\)cm
Kẻ đường cao SH thì H là tâm đường tròn ngoại tiếp tam giác ABC.
Do tam giác ABC đều nên H là trọng tâm tam giác ABC. Gọi D là trung điểm BC
Áp dụng định lý Pytago trong tam giác vuông ABD ta được AD=\(3\sqrt{3}\)cm
\(\Rightarrow AH=\dfrac{2}{3}AD=2\sqrt{3}cm\)
Áp dụng định lý Pytago trong tam giác vuông SHA ta được SH=\(\sqrt{3}\)cm
Thể tích hình chóp là: \(V=\dfrac{1}{3}.\left(\dfrac{1}{2}.6.3\sqrt{3}\right).\sqrt{3}=9\left(cm^2\right)\)
