Cho tam giác ABC. Gọi M là điểm trên cạnh AB sao cho \(\overrightarrow{AM}=\dfrac{1}{4}\overrightarrow{AB}\) và N là điểm trên cạnh CB sao cho
\(\overrightarrow{CN}=\dfrac{3}{5}\overrightarrow{CB}\) . Hãy biểu diễn vecto \(\overrightarrow{MN}\) qua hai vecto \(\overrightarrow{CB}=\overrightarrow{b},\overrightarrow{CA}=\overrightarrow{a}\)
\(\overrightarrow{MN}=\dfrac{3\overrightarrow{b}-11\overrightarrow{a}}{20}\) \(\overrightarrow{MN}=\dfrac{5\overrightarrow{b}-13\overrightarrow{a}}{20}\) \(\overrightarrow{MN}=\dfrac{7\overrightarrow{b}-15\overrightarrow{a}}{20}\) \(\overrightarrow{MN}=\dfrac{9\overrightarrow{b}-17\overrightarrow{a}}{20}\) Hướng dẫn giải: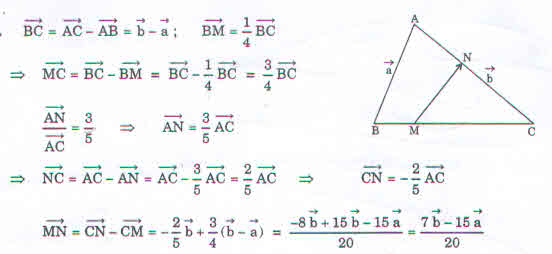

Từ giả thiết suy ra M là trung điểm của AP; P là trung điểm của AB. do đó:
\(\overrightarrow{NM}=\dfrac{1}{2}\left(\overrightarrow{NA}+\dfrac{1}{2}\left(\overrightarrow{NA}+\overrightarrow{NB}\right)\right)=\dfrac{3}{4}\overrightarrow{NA}+\dfrac{1}{4}\overrightarrow{NB}=\dfrac{3}{4}\left(\overrightarrow{CA}-\overrightarrow{CN}\right)+\dfrac{1}{4}.\dfrac{2}{5}\overrightarrow{CB}=\dfrac{3}{4}\left(\overrightarrow{a}-\dfrac{3}{5}\overrightarrow{b}\right)+\dfrac{1}{10}\overrightarrow{b}\)
