Cho tam giác \(ABC\) có \(\widehat{A}=90^0\). Tia phân giác \(BD\) của góc \(B\) (\(D\in AC\)). Trên cạnh \(BC\) lấy điểm \(E\) sao cho \(BE=BA\). Hai góc nào sau đây bằng nhau?
\(\widehat{EDC}\) và \(\widehat{BAC}\).\(\widehat{EDC}\) và \(\widehat{ACB}\).\(\widehat{EDC}\) và \(\widehat{ABC}\).\(\widehat{EDC}\) và \(\widehat{ECD}\).Hướng dẫn giải: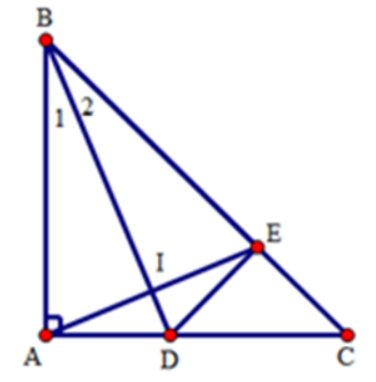
Xét \(\Delta BDA\) và \(\Delta BDE\) có:
\(BA=BE\) (gt)
\(\widehat{B_1}=\widehat{B_2}\) (do \(BD\) là phân giác góc \(B\))
\(BD\) chung
\(\Rightarrow\) \(\Delta BDA=\Delta BDE\) (c.g.c)
\(\Rightarrow\widehat{BAD}=\widehat{BED}=90^0\) (hai góc tương ứng)
Khi đó ta có: \(\widehat{ABC}+\widehat{C}=90^0\) và \(\widehat{EDC}+\widehat{C}=90^0\)
\(\Rightarrow\widehat{EDC}=\widehat{ABC}\)
