Cho một tam giác ABC có AB = 6; AC = 8; BC = 5; M là điểm trên cạnh AB sao cho \(\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}\) , N là
điểm trên cạnh BC sao cho \(\overrightarrow{NB}=-4.\overrightarrow{NC}\). Tính độ dài đoạn MN .
\(\frac{2}{5}\sqrt{205}\) \(\frac{2}{5}\sqrt{210}\) \(\frac{2}{5}\sqrt{215}\) \(\frac{2}{5}\sqrt{220}\) Hướng dẫn giải: ">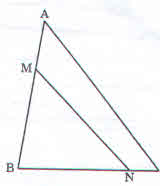
Theo giả thiết ta có: \(AB=6,AC=8,BC=5\); \(\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}\Rightarrow BM'=4\) và
\(\overrightarrow{NB}=-4\overrightarrow{NC}\Rightarrow\overrightarrow{BN}=\dfrac{4}{5}\overrightarrow{BC}\Rightarrow BN=\dfrac{4}{5}.BC=4\) .
Từ tam giác ABC ta có :
\(\cos B=\frac{BA^2+BC^2-AC^2}{2BA.BC}=\frac{36+25-64}{2.6.5}=-\frac{3}{60}=-\frac{1}{20}\)
Từ tam giác BMN ta lại có:
\(MN^2=BM^2+BN^2-2BM.BN.\cos B\)
\(=16+16-2.4.4\left(-\frac{1}{20}\right)=32+\frac{8}{5}=\frac{168}{5}\)
\(\Rightarrow MN=2\sqrt{\frac{42}{5}}=\frac{2}{5}\sqrt{210}\)
Kết luận: \(MN=\dfrac{2}{5}\sqrt{210}\).
