Cho hình lăng trụ đứng \(ABC.A'B'C'\), \(AB=5cm\), \(AC=12cm\), \(BC=13cm\). Có bao nhiêu mặt phẳng vuông góc với mặt phẳng \(\left(ABB'A'\right)\)?
1.2.3.4.Hướng dẫn giải: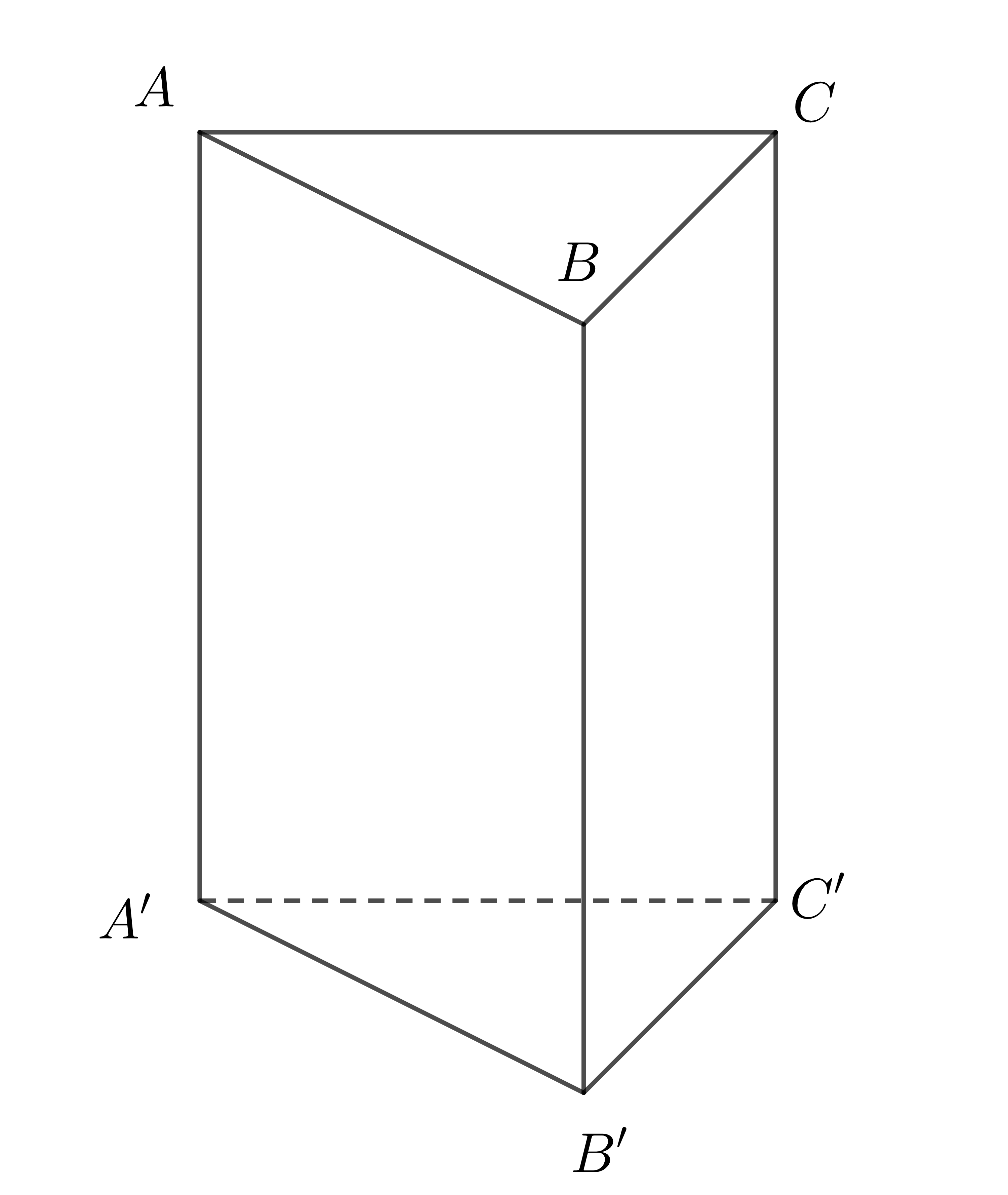
Có \(AB^2+AC^2=5^2+12^2=169=13^3=BC^2\)
Suy ra tam giác ABC vuông tại A.
Do AC vuông góc với hai đường thẳng cắt nhau AB,AA' nên \(AC\perp mp\left(ABB'A'\right)\) do đó \(mp\left(ACC'A'\right)\perp mp\left(ABB'A'\right)\)
Vậy có 3 mp vuông góc với mp(ABB'A') là: (ACC'A'), (ABC), (A'B'C')
