Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), \(SA\perp\left(ABCD\right)\) và \(SA=a\). Khoảng cách giữa hai đường thẳng \(BD\) và \(SC\) là
\(\dfrac{a\sqrt{6}}{6}\).\(\dfrac{a\sqrt{6}}{3}\).\(\dfrac{a\sqrt{3}}{2}\).\(\dfrac{a\sqrt{3}}{3}\).Hướng dẫn giải: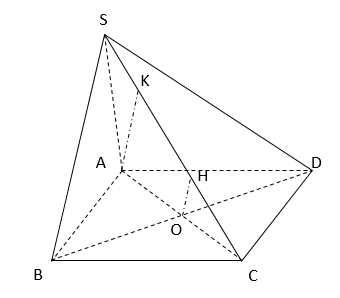
Ta có \(BD\) vuông góc với mp\(\left(SAC\right)\) tại tâm \(O\) của hình vuông \(ABCD\).
Trong mp \(\left(SAC\right)\), kẻ \(OH\) vuông góc với \(SC\) thì \(OH\) là đường vuông góc chung của \(BD\) và \(SC\). Dễ thấy \(d\left(BD;SC\right)=OK=\dfrac{1}{2}AK\)( \(AK\) là đường cao của tam giác vuông \(SAC\)).
Ta có: \(\dfrac{1}{AI^2}=\dfrac{1}{AS^2}+\dfrac{1}{AC^2}=\dfrac{1}{a^2}+\dfrac{1}{2a^2}\).
Nên \(AI=\dfrac{a\sqrt{6}}{3}\), từ đó \(d\left(BD;SC\right)=\dfrac{a\sqrt{6}}{6}\).
