Bài tập cuối chương III
Nội dung lý thuyết
Các phiên bản khácA. NHẮC LẠI LÝ THUYẾT
| Tên hình | Hình vẽ | Chu vi | Diện tích |
Tam giác đều |
| \(C=3a\) (a là cạnh của tam giác) | \(S=\dfrac{1}{2}a.h\) (h là chiều cao) |
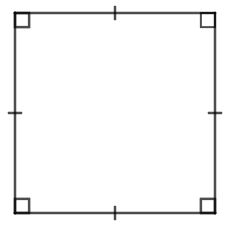
| Hình vuông |
| \(C=4a\) (a là cạnh của hình vuông) | \(S=a.a\) |
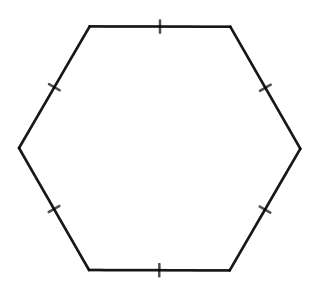
| Lục giác đều |
| \(C=6a\) (a là cạnh của lục giác) | |
| Hình chữ nhật |
| \(C=2\left(a+b\right)\) (a, b là độ dài hai cạnh) | \(S=a.b\) |
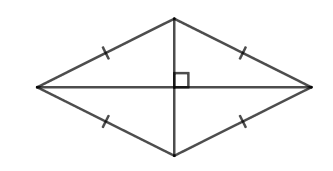
| Hình thoi |
| \(C=4a\) (a là độ dài cạnh của hình thoi) | \(S=\dfrac{1}{2}.m.n\) (m, n là độ dài hai đường chéo của hình thoi) |
| Hình bình hành |
| \(C=2\left(a+b\right)\) (a, b là độ dài hai cạnh) | \(S=a.h\) (h là chiều cao ứng với cạnh a) |
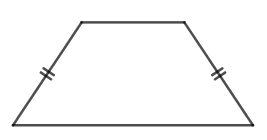
| Hình thang cân |
| \(C=a+b+2c\) (a, b, c lần lượt là độ dài đáy bé, đáy lớn, cạnh bên của hình thang cân) | \(S=\dfrac{1}{2}.\left(a+b\right).h\) (h là chiều cao của hình thang) |
| Hình có trục đối xứng | Hình có tâm đối xứng | Đối xứng trong thực tiễn |
Đoạn thẳng AB có duy nhất một trục đối xứng là đường thẳng d đi qua trung điểm của đoạn AB và vuông góc với AB.
| Đoạn thẳng AB có tâm đối xứng là trung điểm M của đoạn thẳng đó.
|
|
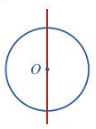
Đường tròn là hình có nhiều trục đối xứng và mỗi trục đối xứng là một đường thẳng đi qua tâm của nó.
| Tâm đối xứng của đường tròn chính là tâm của đường tròn đó.
|
|
Hình thang cân có một trục đố xứng là đường thẳng đi qua trung điểm của hai cạnh đáy.
| Hình thoi, hình chữ nhật, hình vuông, hình bình hành có tâm đối xứng là giao điểm của hai đường chéo.
|
|
Hình lục giác đều có 6 trục đối xứng.
| Hình lục giác đều có tâm đối xứng là điểm O.
|
|
B. BÀI TẬP SGK
1. Tạo ra hình hộp có nắp
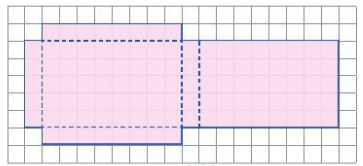
Hãy vẽ các hình chữ nhật trên một miếng bìa mỏng theo cách như ở Hình 96, sau đó cắt, gấp lại và dán mép để tạo thành hình hộp có nắp.
Giải:


2. Cho các hình sau đây:
(1) Đoạn thẳng AB;
(2) Tam giác đều ABC;
(3) Hình tròn tâm O;
(4) Hình thang cân ABCD (có đáy lớn CD);
(5) Hình thoi ABCD.
Trong các hình nói trên:
a) Hình nào có trục đối xứng? Chỉ ra trục đối xứng của hình đó.
b) Hình nào có tâm đối xứng? Chỉ ra tâm đối xứng của hình đó.
Giải:
a) Các hình có trục đối xứng là (1), (2), (3), (4), (5).
- Trục đối xứng của đoan thẳng AB là đường thẳng d:
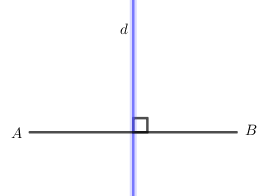
- Tam giác đều ABC có ba trục đối xứng:

- Hình tròn tâm O có vô số trục đối xứng. Mỗi trục đối xứng là đường thẳng đi qua tâm
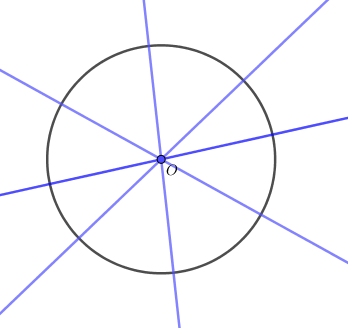
- Hình thang cân ABCD có một trục đối xứng là đường thẳng đi qua trung điểm hai cạnh đáy.

- Hình thoi ABCD có hai trục đối xứng là hai đường chéo của hình thoi:
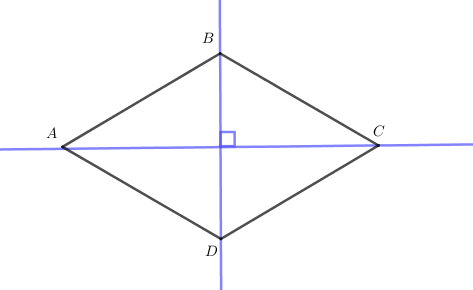
b) Các hình có tâm đối xứng là: (1), (3), (5).
Tâm đối xứng của đoạn thẳng AB chính là trung điểm của đoạn thẳng AB.
Tâm đối xứng của hình tròn tâm O chính là tâm O.
Tâm đối xứng của hình thoi ABCD chính là giao điểm của hai đường chéo AC và BD.
3. Hãy quan sát xung quanh và chỉ ra những hình:
a) Có trục đối xứng;
b) Có tâm đối xứng;
c) Vừa có trục đối xứng vừa có tâm đối xứng.
Giải:
a) Những hình có trục đối xứng:
Cổng nhà |
Tháp Eiffel |
b) Những hình có tâm đối xứng:
|
|
c) Những hình vừa có trục đối xứng vừa có tâm đối xứng:

4. Hãy tìm và kể tên một số ứng dụng của tính đối xứng mà em biết.
5.
a) Một hình thoi có cạnh 4 cm thì chu vi của nó bằng bao nhiêu?
b) Một hình vuông có chu vi là 40 cm thì cạnh của nó bằng bao nhiêu?
c) Một hình chữ nhật có chu vi 30 cm và chiều rộng 7 cm thì chiều dài của nó bằng bao nhiêu?
d) Một hình chữ nhật có chu vi 36 cm và chiều dài gấp đôi chiều rộng thì mỗi cạnh của nó bằng bao nhiêu?
Giải:
a) Chi vi của hình thoi là: 4.4 = 16 (cm).
b) Cạnh của hình vuông là: 40 : 4 = 10 (cm).
c) Tổng chiều dài và chiều rộng của hình chữ nhật là 30 : 2 = 15 (cm)
Chiều dài của hình chữ nhật là: 15 - 7 = 8 (cm).
d) Vì chiều dài = 2. chiều rộng.
Mà (chiều dài + chiều rộng) . 2 = 36.
Do đó: 3.chiều rộng = 18
chiều rộng = 18 : 3 = 6 cm.
Khi đó chiều dài = 12 cm.
6. Sử dụng thước, hãy đo và cho biết chu vi của một số đồ vật có dạng hình chữ nhật trong thực tiễn. Chẳng hạn, đo chu vi mặt bàn học của em; đo chu vi bìa một quyển sách mà em có.
Giải:
Quyển vở kẻ ngang có kích thước là 17 cm và 27 cm.
Chu vi quyển vở là 2.(17+25) = 84 cm.
7. Quan sát hình 97, hình 98 và tính diện tích phần tô xanh ở mỗi hình đó.
.png)
Giải:
* Hình 97:
Diện tích hình đã cho bằng tổng diện tích của bốn hình nhỏ gồm hình vuông, hình chữ nhật, hình thoi, hình thang vuông:
\(S=12.12+\dfrac{1}{2}\left(12+12\right).\left(5+5\right)+12.3+\dfrac{1}{2}\left(13+15\right).11\)
\(=144+120+36+154=454\) cm2.
Vậy diện tích của hình 97 là 454 cm2.
* Hình 98:
Diện tích hình đã cho bằng tổng diện tích của ba hình nhỏ gồm hình tam giác, hình chữ nhật, hình bình hành:
\(S=\dfrac{1}{2}.45.18+20.45+15.45=1980\) cm2.
Vậy diện tích của hình 98 là 1980 cm2.
8. Trên mảnh đất có dạng hình chữ nhật với chiều dài là 28 m, chiều rộng là 24 m, người ta định xây dựng một vườn hoa hình chữ nhật và bớt ra một phần đường đi như ở hình 99.
a) Tính diện tích mảnh đất có dạng hình chữ nhật đó. b) Tính diện tích vườn hoa. c) Người ta định dùng những viên gạch chống trượt có dạng hình vuông có cạnh là 50 cm để lát đường đi. Cần dùng bao nhiêu viên gạch như thế. Biết rằng diện tích các mỗi nối và sự hao hụt là không đáng kể. |
|
Giải:
a) Diện tích mảnh đất là 28.24 = 672 m2.
b) Chiều dài vườn hoa là 28 - 1 = 27 m.
Chiều rộng vườn hoa là 24 - 1 = 23 m.
Diện tích vườn hoa là 27.23 = 621 m2.
c) Diện tích phần đường đi là 672 - 621 = 51 m2.
Diện tích một viên gạch hình vuông là 50.50 = 2500 cm2 = 0,25 m2.
Cần số viên gạch là 51 : 0,25 = 204 viên.
9.
Bạn Thảo muốn cắt miếng bìa màu xanh có diện tích là 28 cm2 như Hình 100. Biết chu vi hình vuông ABCD là 16 cm. Tính giúp bạn Thảo độ dài cạnh EG.
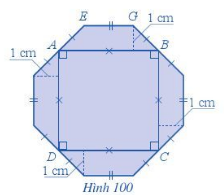
Giải:
Miếng bìa gồm 1 hình vuông ABCD và 4 hình thang cân có diện tích bằng nhau.
Độ dài cạnh AB là 16 : 4 = 4 cm.
Diện tích hình vuông ABCD là 4.4 = 16 cm2.
Diện tích bốn hình thang cân là 28 - 16 = 12 cm2.
Diện tích hình thang cân EGBA là 12 : 4 = 3 cm2.
Độ dài cạnh EG là \(\dfrac{3.2}{1}-4=2\) cm.

.png)

.png)