Bài 7: Trường hợp đồng dạng thứ ba
Nội dung lý thuyết
Các phiên bản khác1. Định lí
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Xét bài toán: Cho \(\Delta ABC\) và \(\Delta A'B'C'\) có \(\widehat{A}=\widehat{A'}\), \(\widehat{B}=\widehat{B'}\). Khi đó \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\).
Chứng minh:
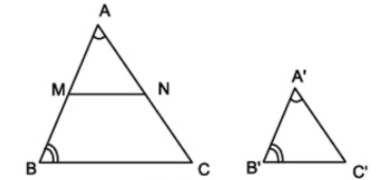
Trên tia \(AB\) lấy điểm \(M\) sao cho \(AM=A'B'\). Qua \(M\) kẻ song song với \(BC\) cắt \(AC\) tại \(N\).
Xét \(\Delta ABC\) có \(M\in AB,N\in AC\) mà \(MN\)//\(BC\)
Suy ra \(\Delta AMN\) đồng dạng với \(\Delta ABC\) (1)
Mặt khác ta có \(\widehat{AMN}=\widehat{B}\) (hai góc đòng vị) mà \(\widehat{B}=\widehat{B'}\) \(\Rightarrow\widehat{AMN}=\widehat{B'}\)
Xét \(\Delta AMN\) và \(\Delta A'B'C'\) có:
\(\widehat{A}=\widehat{A'}\) (gt)
\(AM=A'B'\) (cách dựng)
\(\widehat{AMN}=\widehat{B'}\)
Suy ra \(\Delta AMN=\Delta A'B'C'\) (2)
Từ (1) và (2) \(\Rightarrow\) \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\).
Ví dụ:
+) Nếu \(\Delta DEF\) và \(\Delta MNP\) có
\(\widehat{D}=\widehat{M}\) ; \(\widehat{F}=\widehat{P}\)
thì \(\Delta DEF\) đồng dạng với \(\Delta MNP\) ;
+) Nếu \(\Delta HIK\) và \(\Delta GOM\) có
\(\widehat{I}=\widehat{O}\) ; \(\widehat{K}=\widehat{M}\)
thì \(\Delta HIK\) đồng dạng với \(\Delta GOM\) ;
+) Nếu \(\Delta RSK\) và \(\Delta TQP\) có
\(\widehat{R}=\widehat{Q}\) ; \(\widehat{S}=\widehat{P}\)
thì \(\Delta RSK\) đồng dạng với \(\Delta PQT\).
2. Áp dụng
Ví dụ 1: Cho tam giác \(ABC\) có \(\widehat{A}=60^0\), \(\widehat{C}=50\). Tam giác \(A'B'C'\) có \(\widehat{B'}=70^0\), \(\widehat{A'}-\widehat{C'}=10^0\).
Chứng minh rằng hai tam giác trên đồng dạng vơi nhau?
Giải:
Xét \(\Delta ABC\) ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\) (tổng ba góc trong tam giác bằng \(180^0\))
\(\Rightarrow\widehat{B}=180^0-\widehat{A}-\widehat{C}=180^0-50^0-60^0=70^0\)
Xét \(\Delta A'B'C'\) ta có: \(\widehat{A'}+\widehat{B'}+\widehat{C'}=180^0\) (tổng ba góc trong tam giác bằng \(180^0\))
\(\Rightarrow\widehat{A'}+\widehat{C'}=180^0-70^0=110^0\) mà \(\widehat{A'}-\widehat{C'}=10^0\)
\(\Rightarrow\widehat{A'}=\dfrac{110^0+10^0}{2}=\dfrac{120^0}{2}=60^0\)
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) có:
\(\widehat{A}=\widehat{A'}=60^0\)
\(\widehat{B}=\widehat{B'}=70^0\)
Suy ra \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\) (g.g)
Ví dụ 2: Cho \(\Delta ABC\) có đường cao \(AD,CE\) cắt nhau tại \(H\). Chứng minh rằng:
a) \(\Delta ABD\) đồng dạng với \(\Delta CBE\)
b) \(\Delta AHE\) đồng dạng với \(\Delta CBE\)
Giải:
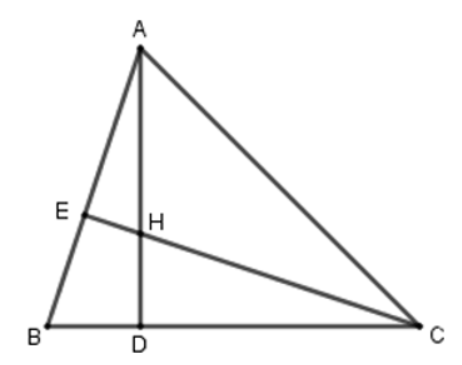
a) Do \(AD,CE\) là đường cao của \(\Delta ABC\) \(\Rightarrow\) \(AD\perp BC\) và \(CE\perp AB\)
Xét \(\Delta ABD\) và \(\Delta CBE\) có:
\(\widehat{D}=\widehat{E}=90^0\) (do \(AD\perp BC\), \(CE\perp AB\))
\(\widehat{B}\) chung
Suy ra \(\Delta ABD\) đồng dạng với \(\Delta CBE\) (g.g)
b) Do \(\Delta ABD\) đồng dạng với \(\Delta CBE\)
\(\Rightarrow\widehat{BAD}=\widehat{BCE}\) (hai góc tương ứng) hay \(\widehat{EAH}=\widehat{BCE}\)
Xét \(\Delta AHE\) và \(\Delta CBE\) có:
\(\widehat{EAH}=\widehat{BCE}\) (cmt)
\(\widehat{AEH}=\widehat{CEB}=90^0\)
Suy ra \(\Delta AHE\) đồng dạng với \(\Delta CBE\) (g.g)
@59168@
Ví dụ 3: Cho tam giác \(ABC\) có \(AB=6cm,AC=9cm\). Trên cạnh \(AC\) lấy điểm \(D\) sao cho \(\widehat{ABD}=\widehat{ACB}\). Đặt \(AD=x\left(cm\right)\). Tính \(x\)?
Giải:
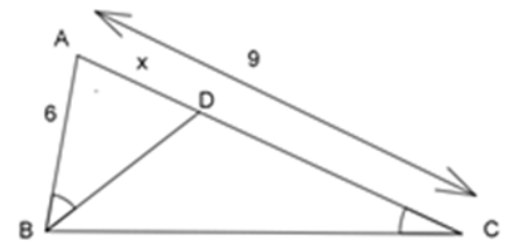
Xét \(\Delta ABD\) và \(\Delta ACB\) có:
\(\widehat{A}\) chung
\(\widehat{ABD}=\widehat{ACB}\) (gt)
\(\Rightarrow\) \(\Delta ABD\) đồng dạng với \(\Delta ACB\) (g.g)
\(\Rightarrow\) \(\dfrac{AB}{AD}=\dfrac{AC}{AB}\)
\(\Rightarrow\) \(\dfrac{6}{x}=\dfrac{9}{6}\Rightarrow x=\dfrac{6.6}{9}=\dfrac{36}{9}=4\)
Vậy \(x=4\left(cm\right)\).
Ví dụ 4: Cho hình thang \(ABCD\) (\(AB\)//\(CD\)), biết \(AB=12,5cm\), \(CD=28,5cm\). Góc \(\widehat{BAD}\) bằng góc \(\widehat{CBD}\). Tính độ dài đường chéo \(BD\)?
Giải:
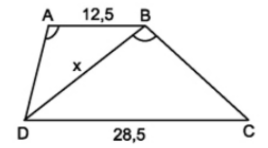
Do \(AB\)//\(CD\) \(\Rightarrow\widehat{ABD}=\widehat{BDC}\) (hai góc so le trong)
Xét \(\Delta ABD\) và \(\Delta BDC\) có:
\(\widehat{ABD}=\widehat{BDC}\) (cmt)
\(\widehat{BAD}=\widehat{CBD}\) (gt)
Suy ra \(\Delta ABD\) đồng dạng với \(\Delta BDC\) (g.g)
\(\Rightarrow\) \(\dfrac{AB}{BD}=\dfrac{BD}{DC}\)
\(\Rightarrow BD^2=AB.DC=12,5.28.5\)
\(\Rightarrow BD=\sqrt{12,5.28,5}\approx18,87\) (cm)
Vậy \(BD\approx18,87cm\)
@1508663@@1507724@