Bài 6: Ôn tập chương Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Nội dung lý thuyết
Các phiên bản khácI. SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ
1. Tính đơn điệu của hàm số
Kí hiệu \(K\) là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số \(y=f\left(x\right)\) xác định trên \(K\).
Hàm số \(y=f\left(x\right)\) đồng biến (tăng) trên \(K\) nếu với mọi cặp \(x_1,x_2\in K\) và \(x_1< x_2\) thì \(f\left(x_1\right)< f\left(x_2\right)\), tức là \(x_1< x_2\Rightarrow f\left(x_1\right)< f\left(x_2\right)\) ;
Hàm số \(y=f\left(x\right)\) nghịch biến (giảm) trên \(K\) nếu với mọi cặp \(x_1,x_2\in K\) và \(x_1< x_2\) thì \(f\left(x_1\right)>f\left(x_2\right)\), tức là \(x_1< x_2\Rightarrow f\left(x_1\right)>f\left(x_2\right)\).
Hàm số đồng biến hoặc nghịch biến trên \(K\) được gọi chung là hàm số đơn điệu trên \(K\).
Nhận xét:
a) \(f\left(x\right)\) đồng biến trên \(K\) \(\Leftrightarrow\dfrac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}>0\), \(\forall x_1,x_2\in K\) , (\(x_1\ne x_2\)) ;
\(f\left(x\right)\) nghịch biến trên \(K\) \(\Leftrightarrow\dfrac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}< 0\), \(\forall x_1,x_2\in K\), (\(x_1\ne x_2\)).
b) Nếu hàm số đồng biến trên \(K\) thì đồ thị đi lên từ trái sang phải ;
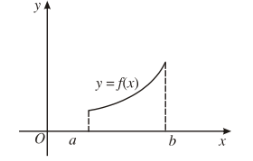
Nếu hàm số nghịch biến trên \(K\) thì đồ thị đi xuống từ trái sang phải.
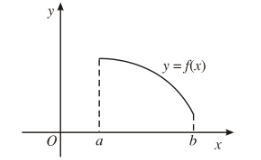
2. Tính đơn điệu và dấu của đạo hàm
Cho hàm số \(y=f\left(x\right)\) có đạo hàm trên \(K\).
a) Nếu \(f'\left(x\right)>0\) với mọi \(x\in K\) thì hàm số \(f\left(x\right)\) đồng biến trên \(K\).
b) Nếu \(f'\left(x\right)< 0\) với mọi \(x\in K\) thì hàm số \(f\left(x\right)\) nghịch biến trên \(K\).
Chú ý: Nếu \(f'\left(x\right)=0\), \(\forall x\in K\) thì \(f\left(x\right)\) không đổi trên \(K\).
Chú ý: Ta có định lí mở rộng sau đây:
Giả sử hàm số \(y=f\left(x\right)\) có đạo hàm trên \(K\). Nếu \(f'\left(x\right)\ge0\) (\(f'\left(x\right)\le0\)), \(\forall x\in K\) và \(f'\left(x\right)=0\) chỉ tại một số hữu hạn điểm thì hàm số đồng biến (nghịch biến) trên \(K\).
3. Quy tắc xét tính đơn điệu của hàm số
1. Tìm tập xác định.
2. Tính đạo hàm \(f'\left(x\right)\). Tìm các điểm \(x_i\left(i=1,2,3,...,n\right)\) mà tại đó đạo hàm bằng 0 hoặc không xác định.
3. Sắp xếp các điểm \(x_i\) theo thứ tự tăng dần và lập bảng biến thiên.
4. Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
@2323499@
II. CỰC TRỊ CỦA HÀM SỐ
1. Khái niệm cực đại, cực tiểu
Cho hàm số \(y=f\left(x\right)\) xác định và liên tục trên khoảng \(\left(a;b\right)\) (có thể \(a\) là \(-\infty\), \(b\) là \(+\infty\)) và điểm \(x_0\in\left(a;b\right)\).
a) Nếu tồn tại số \(h>0\) sao cho \(f\left(x\right)< f\left(x_0\right)\) với mọi \(x\in\left(x_0-h;x_0+h\right)\) và \(x\ne x_0\) thì ta nói hàm số \(f\left(x\right)\) đạt cực đại tại \(x_0\).
b) Nếu tồn tại số \(h>0\) sao cho \(f\left(x\right)>f\left(x_0\right)\) với mọi \(x\in\left(x_0-h;x_0+h\right)\) và \(x\ne x_0\) thì ta nói hàm số \(f\left(x\right)\) đạt cực tiểu tại \(x_0\).
Chú ý:
1. Nếu hàm số \(f\left(x\right)\) đạt cực đại (cực tiểu) tại \(x_0\) thì \(x_0\) được gọi là điểm cực đại (điểm cực tiểu) của hàm số, \(f\left(x_0\right)\) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, kí hiệu là \(f_{CĐ}\left(f_{CT}\right)\), còn điểm \(M\left(x_0;f\left(x_0\right)\right)\) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.
2. Các điểm cực đại và cực tiểu được gọi chung là các điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn được gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.
3. Dễ dàng chứng minh được rằng, nếu hàm số \(y=f\left(x\right)\) có đạo hàm trên khoảng \(\left(a;b\right)\) và đạt cực đại hoặc cực tiểu tại \(x_0\) thì \(f'\left(x_0\right)=0\).
2. Điều kiện để hàm số có cực trị
Định lí 1:
Giả sử hàm số \(y=f\left(x\right)\) liên tục trên khoảng \(K=\left(x_0-h;x_0+h\right)\) và có đạo hàm trên \(K\) hoặc trên \(K\)\\(\left\{x_0\right\}\), với \(h>0\).
a) Nếu \(f'\left(x\right)>0\) trên khoảng \(\left(x_0-h;x_0\right)\) và \(f'\left(x\right)< 0\) trên khoảng \(\left(x_0;x_0+h\right)\) thì \(x_0\) là một điểm cực đại của hàm số \(f\left(x\right)\).
b) Nếu \(f'\left(x\right)< 0\) trên khoảng \(\left(x_0-h;x_0\right)\) và \(f'\left(x\right)>0\) trên khoảng \(\left(x_0;x_0+h\right)\) thì \(x_0\) là một điểm cực tiểu của hàm số \(f\left(x\right)\).
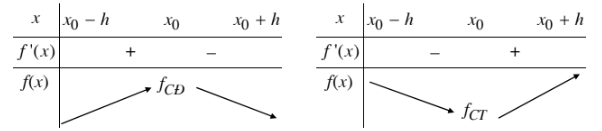
3. Quy tắc tìm cực trị
Quy tắc 1:
1. Tìm tập xác định.
2. Tính \(f'\left(x\right)\). Tìm các điểm tại đó \(f'\left(x\right)=0\) hoặc \(f'\left(x\right)\) không xác định.
3. Lập bảng biến thiên.
4. Từ bảng biến thiên suy ra các điểm cực trị.
Định lí 2:
GIả sử hàm số \(y=f\left(x\right)\) có đạo hàm cấp hai trong khoảng \(\left(x_0-h;x_0+h\right)\) với \(h>0\). Khi đó:
a) Nếu \(f'\left(x_0\right)=0,f''\left(x_0\right)>0\) thì \(x_0\) là điểm cực tiểu;
b) Nếu \(f'\left(x_0\right)=0,f''\left(x_0\right)< 0\) thì \(x_0\) là điểm cực đại.
Quy tắc 2:
1. Tìm tập xác định.
2. Tính \(f'\left(x\right)\). Giải phương trình \(f'\left(x\right)=0\) và kí hiệu \(x_i\left(i=1,2,...,n\right)\) là các nghiệm của nó.
3. Tính \(f''\left(x\right)\) và \(f''\left(x_i\right)\).
4. Dựa vào dấu của \(f''\left(x_i\right)\) suy ra tính chất cực trị của điểm \(x_i\).
III. GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
1. Định nghĩa
Cho hàm số \(y=f\left(x\right)\) xác định trên tập \(D\)
a) Số \(M\) được gọi là giá trị lớn nhất của hàm số \(y=f\left(x\right)\) trên tập \(D\) nếu \(f\left(x\right)\le M\) với mọi \(x\) thuộc \(D\) và tồn tại \(x_0\in D\) sao cho \(f\left(x_0\right)=M\).
Kí hiệu: \(M=\max\limits_Df\left(x\right)\)
b) Số \(m\) được gọi là giá trị nhỏ nhất của hàm số \(y=f\left(x\right)\) trên tập \(D\) nếu \(f\left(x\right)\ge m\) với mọi \(x\) thuộc \(D\) và tồn tại \(x_0\in D\) sao cho \(f\left(x_0\right)=m\).
Kí hiệu: \(m=\min\limits_Df\left(x\right)\).
2. Cách tính giá trị lớn nhất và giá trị nhỏ nhất trên một đoạn
a) Định lí: Mọi hàm số liên tục trên một đoạn đều có giá trị nhỏ nhất và giá trị lớn nhất trên đoạn đó.
b) Quy tắc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số liên tục trên một đoạn
Nhận xét:
Nếu đạo hàm \(f'\left(x\right)\) giữ nguyên dấu trên đoạn \(\left[a;b\right]\) thì hàm số đồng biến hoặc nghịch biến trên cả đoạn. Do đó \(f\left(x\right)\) đạt được giá trị nhỏ nhất và giá trị lớn nhất tại các đầu mút của đoạn.
Nếu chỉ có một số hữu hạn các điểm \(x_i\left(x_i< x_{i+1}\right)\) mà tại đó \(f'\left(x\right)\) bằng 0 hoặc không xác định thì hàm số \(y=f\left(x\right)\) đơn điệu trên mỗi khoảng \(\left(x_i;x_{i+1}\right)\). Rõ ràng giá trị lớn nhất (giá trị nhỏ nhất) của hàm số trên đoạn \(\left[a;b\right]\) là số lớn nhất (số nhỏ nhất) trong các giá trị của hàm số tại hai đầu mút \(a,b\) và các điểm \(x_i\) nói trên.
Quy tắc:
1. Tìm các điểm \(x_1,x_2,...,x_n\) trên khoảng \(\left(a,b\right)\) mà tại đó \(f'\left(x\right)\) bằng 0 hoặc không xác định.
2. Tính \(f\left(a\right),f\left(x_1\right),f\left(x_2\right),...,f\left(x_n\right),f\left(b\right)\).
3. Tìm số lớn nhất \(M\) và số nhỏ nhất \(m\) trong các số trên. Ta có
\(M=\max\limits_{\left[a;b\right]}f\left(x\right),m=\min\limits_{\left[a;b\right]}f\left(x\right)\)
Chú ý: Hàm số liên tục trên một khoảng có thể không có giá trị lớn nhất và giá trị nhỏ nhất trên khoảng đó.
@2324699@
IV. ĐƯỜNG TIỆM CẬN
1. Đường tiệm cận ngang
Định nghĩa:
Cho hàm số \(y=f\left(x\right)\) xác định trên một khoảng vô hạn (là khoảng dạng \(\left(a;+\infty\right)\), \(\left(-\infty;b\right)\) hoặc \(\left(-\infty;+\infty\right)\)). Đường thẳng \(y=y_0\) là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số \(y=f\left(x\right)\) nếu ít nhất một trong các điều kiện sau được thoả mãn
\(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=y_0\) ; \(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=y_0\).
Chú ý: Nếu \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=\lim\limits_{x\rightarrow-\infty}f\left(x\right)=a\), ta viết chung là \(\lim\limits_{x\rightarrow\pm\infty}f\left(x\right)=a\) (\(a\in R\)).
2. Đường tiệm cận đứng
Định nghĩa:
Đường thẳng \(x=x_0\) được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số \(y=f\left(x\right)\) nếu ít nhất một trong các điều kiện sau được thoả mãn
\(\lim\limits_{x\rightarrow x_0^+}f\left(x\right)=+\infty\) ; \(\lim\limits_{x\rightarrow x_0^-}f\left(x\right)=-\infty\) ;
\(\lim\limits_{x\rightarrow x_0^+}f\left(x\right)=-\infty\) ; \(\lim\limits_{x\rightarrow x_0^-}f\left(x\right)=+\infty\).
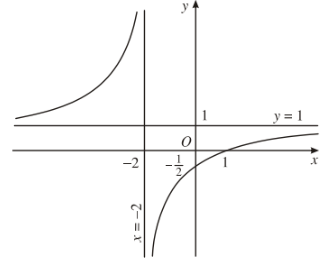
Ví dụ: Tìm các đường tiệm cận đứng và ngang của đồ thị hàm số \(y=\dfrac{x-1}{x+2}\) (C).
Giải:
Vì \(\lim\limits_{x\rightarrow-2^+}\dfrac{x-1}{x+2}=-\infty\) (hoặc \(\lim\limits_{x\rightarrow-2^-}\dfrac{x-1}{x+2}=+\infty\)) nên đường thẳng \(x=-2\) là tiệm cận đứng của (C).
Vì \(\lim\limits_{x\rightarrow\pm\infty}\dfrac{x-1}{x+2}=1\) nên đường thẳng \(y=1\) là tiệm cận ngang của (C).
V. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ HÀM SỐ
1. Sơ đồ khảo sát hàm số
a) Tập xác định
Tìm tập xác định của hàm số.
b) Sự biến thiên
- Xét chiều biến thiên của đồ thị hàm số:
+ Tính đạo hàm \(y'\) ;
+ Tìm các điểm tại đó đạo hàm \(y'\) bằng 0 hoặc không xác định ;
+ Xét dấu đạo hàm \(y'\) và suy ra chiều biến thiên của đồ thị hàm số.
- Tìm cực trị.
- Tìm các giới hạn tại vô cực, các giới hạn vô cực và các tiệm cận (nếu có).
- Lập bảng biến thiên. (Ghi các kết quả tìm được vào bảng biến thiên).
c) Đồ thị
Dựa vào bảng biến thiên và các yếu tố xác định ở trên để vẽ đồ thị.
Chú ý:
+) Nếu hàm số tuần hoàn với chu kì \(T\) thì chỉ cần khảo sát sự biến thiên và vẽ đồ thị trên một chu kì, sau đó tịnh tiến đồ thị song song với trục \(Ox\).
+) Nên tính thêm toạ độ một số điểm, đặc biệt là toạ độ giao điểm của đồ thị với hai trục toạ độ.
+) Nên lưu ý đến tính chẵn lẻ của hàm số và tính đối xứng của đồ thị để vẽ cho chính xác.
2. Khảo sát một hàm đa thức và hàm phân thức
a) Hàm số \(y=ax^3+bx^2+cx+d\left(a\ne0\right)\)
Ví dụ 1: Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y=x^3+3x^2-4\).
Giải:
- Tập xác định: \(R\)
- Sự biến thiên:
+ Chiều biến thiên: \(y'=3x^2+6x=3x\left(x+2\right)\). \(y'=0\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=0\end{matrix}\right.\)
Trên các khoảng \(\left(-\infty;-2\right)\) và \(\left(0;+\infty\right)\), \(y'\) dương nên hàm số đồng biến.
Trên khoảng \(\left(-2;0\right)\), \(y'\) âm nên hàm số nghịch biến.
+ Cực trị: Hàm số đạt cực đại tại \(x=-2\), \(y_{CĐ}=y\left(-2\right)=0\)
Hàm số đạt cực tiểu tại \(x=0\), \(y_{CT}=y\left(0\right)=-4\).
+ Các giới hạn tại vô cực:
\(\lim\limits_{x\rightarrow-\infty}y=\lim\limits_{x\rightarrow-\infty}x^3\left(1+\dfrac{3}{x}-\dfrac{4}{x^3}\right)=-\infty\)
\(\lim\limits_{x\rightarrow+\infty}y=\lim\limits_{x\rightarrow+\infty}x^3\left(1+\dfrac{3}{x}-\dfrac{4}{x^3}\right)=+\infty\)
+ Bảng biến thiên:
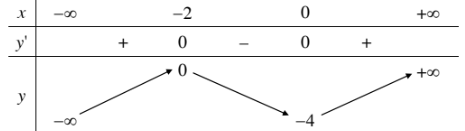
- Đồ thị:
Ta có \(\left(-2;0\right)\) và \(\left(1;0\right)\) là các giao điểm của đồ thị với trục \(Ox\) ; \(\left(0;-4\right)\) là giao điểm của đồ thị với trục \(Oy\).
Lưu ý: Đồ thị hàm số có tâm đối xứng là điểm \(I\left(-1;-2\right)\) (hoành độ của tâm đối xứng đó là nghiệm của phương trình \(y''=0\)).
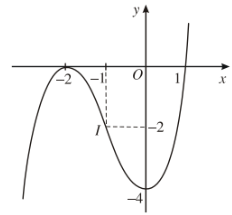
Dạng của đồ thị hàm số bấc ba \(y=ax^3+bx^2+cx+d\left(a\ne0\right)\)
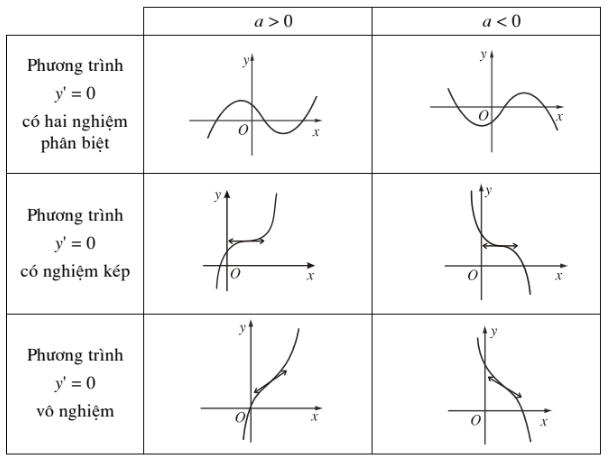
b) Hàm số \(y=ax^4+bx^2+c\left(a\ne0\right)\)
Ví dụ 2: Khảo sát sự biến thiên và vẽ đồ thị hàm số \(y=x^4-2x^2-3\).
Giải:
- Tập xác định: \(R\)
- Sự biến thiên:
Chiều biến thiên: \(y'=4x^3-4x=4x\left(x^2-1\right)\) ; \(y'=0\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=1\\x=0\end{matrix}\right.\)
Trên các khoảng \(\left(-1;0\right)\) và \(\left(1;+\infty\right)\), \(y'>0\) nên hàm số đồng biến.
Trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\), \(y'< 0\) nên hàm số nghịch biến.
Cực trị: Hàm số đạt cực tiểu tại \(x=1\) và \(x=-1\), \(y_{CT}=y\left(\pm1\right)=-4\) ;
Hàm số đạt cực đại tại \(x=0\), \(y_{CĐ}=y\left(0\right)=-3\).
Giới hạn tại vô cực:
\(\lim\limits_{x\rightarrow-\infty}y=\lim\limits_{x\rightarrow-\infty}x^4\left(1-\dfrac{2}{x^2}-\dfrac{3}{x^4}\right)=+\infty\)
\(\lim\limits_{x\rightarrow+\infty}y=\lim\limits_{x\rightarrow+\infty}x^4\left(1-\dfrac{2}{x^2}-\dfrac{3}{x^4}\right)=+\infty\)
Bảng biến thiên:

- Đồ thị: Hàm số đã cho là hàm chẵn nên đồ thị nhận trục \(Oy\) làm trục đối xứng
Đồ thị cắt trục hoành tại các điểm \(\left(\sqrt{3};0\right)\) và \(\left(-\sqrt{3};0\right)\), cắt trục tung tại điểm \(\left(0;-3\right)\).
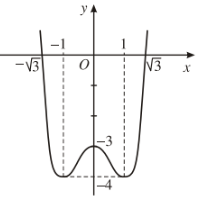
Dạng của đồ thị hàm số \(y=ax^4+bx^2+c\left(a\ne0\right)\)
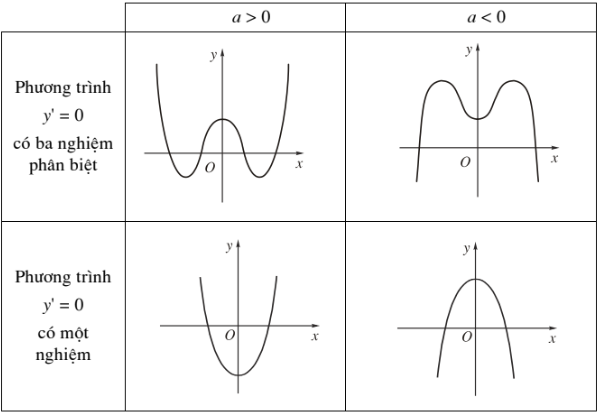
c) Hàm số \(y=\dfrac{ax+b}{cx+d}\left(c\ne0,ad-bc\ne0\right)\)
Ví dụ 3: Khảo sát sự biến thiên và vẽ đồ thị hàm số \(y=\dfrac{-x+2}{x+1}\).
Giải:
- Tập xác định: \(R\backslash\left\{-1\right\}\)
- Sự biến thiên:
Chiều biến thiên: \(y'=-\dfrac{3}{\left(x+1\right)^2}\)
\(y'\) không xác định tại \(x=-1\), luôn âm với mọi \(x\ne-1\)
Vậy hàm số nghịch biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(-1;+\infty\right)\)
Cực trị: Hàm số đã cho không có cực trị
Tiệm cận: \(\lim\limits_{x\rightarrow-1^-}y=\lim\limits_{x\rightarrow-1^-}\dfrac{-x+2}{x+1}=-\infty\), \(\lim\limits_{x\rightarrow-1^+}y=\lim\limits_{x\rightarrow-1^+}\dfrac{-x+2}{x+1}=+\infty\)
Do đó đường thẳng \(x=-1\) là tiệm cận đứng.
\(\lim\limits_{x\rightarrow\pm\infty}y=\lim\limits_{x\rightarrow\pm\infty}\dfrac{-x+2}{x+1}=-1\)
Do đó đường thẳng \(y=-1\) là tiệm cận ngang
Bảng biến thiên:
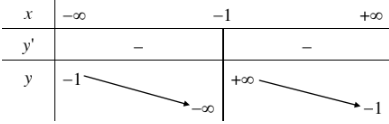
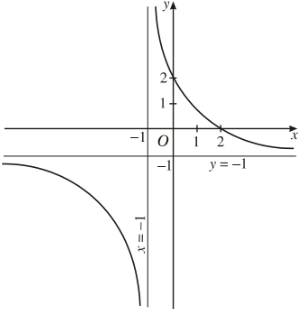
- Đồ thị: Đồ thị cắt trục tung tại điểm \(\left(0;2\right)\) và cắt trục hoành tại điểm \(\left(2;0\right)\)
Lưu ý: Giao điểm của hai tiệm cận là tâm đối xứng của đồ thị.
Dạng của đồ thị \(y=\dfrac{ax+b}{cx+d}\left(c\ne0,ad-bc\ne0\right)\)
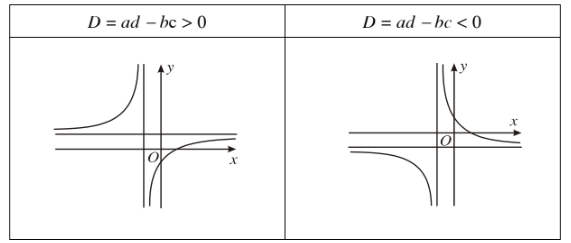
3. Sự tương giao của hai đồ thị
Giả sử hàm số \(y=f\left(x\right)\) có đồ thị \(\left(C_1\right)\) và hàm số \(y=g\left(x\right)\) có đồ thị \(\left(C_2\right)\). Để tìm hoành độ giao điểm của \(\left(C_1\right)\) và \(\left(C_2\right)\) ta giải phương trình \(f\left(x\right)=g\left(x\right)\). Giả sử phương trình trên có các nghiệm là \(x_0,x_1,...\) Khi đó các giao điểm của \(\left(C_1\right)\) và \(\left(C_2\right)\) là \(M_0\left(x_0;f\left(x_0\right)\right)\), \(M_1\left(x_1;f\left(x_1\right)\right)\), ...
Ví dụ 4:
a) Vẽ đồ thị hàm số \(y=x^3+3x^2-2\) ;
b) Sử dụng đồ thị, biện luận theo tham số m số nghiệm của phương trình \(x^3+3x^2-2=m\).
Giải:
a) \(y'=3x^2+6x;y'=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Đồ thị có điểm cực đại là \(\left(-2;2\right)\) và điểm cực tiểu là \(\left(0;-2\right)\)
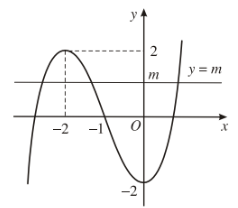
b) Số nghiệm của phương trình \(x^3+3x^2-2=m\) bằng số giao điểm của đồ thị hàm số \(y=x^3+3x^2-2\) và đường thẳng \(y=m\).
Dựa vào đồ thị ta có:
\(m>2\): Phương trình \(x^3+3x^2-2=m\) có một nghiệm ;
\(m=2\): Phương trình \(x^3+3x^2-2=m\) có hai nghiệm ;
\(-2< m< 2\): Phương trình \(x^3+3x^2-2=m\) có ba nghiệm ;
\(m=-2\): Phương trình \(x^3+3x^2-2=m\) có hai nghiệm ;
\(m< -2\): Phương trình \(x^3+3x^2-2=m\) có một nghiệm.
@2324290@
Danh sách các phiên bản khác của bài học này. Xem hướng dẫn