Bài 5: Khảo sát sự biến thiên và vẽ đồ thị hàm số

Khảo sát sự biến thiên và vẽ đồ thị hàm số

I. Sơ đồ khảo sát hàm số (tổng quát)

1. Tập xác định.

  Tìm tập xác định của hàm số

2. Sự biến thiên.

- Xét chiều biến thiên của hàm số

   + Tính đạo hàm y'

   + Tìm các điểm tại đó y' bằng 0 hoặc không xác định

   + Xét dấu đạo hàm y' và suy ra chiều biến thiên của hàm số y

- Tìm cực trị

- Tìm các giới hạn tại vô cực, các giới hạn vô cực và tìm tiệm cận (nếu có)

- Lập bảng biến thiên (Ghi các kết quả tìm được vào bảng biến thiên).

3. Đồ thị.

Dựa vào bảng biến thiên, các yếu tố xác định ở trên để vẽ đồ thị. Có thể khảo sát thêm các yếu tố sau để có đồ thị chính xác hơn:

• Tương giao với các trục.

• Tính đối xứng (nếu có).

• Điểm đặc biệt (nếu cần).

• Điểm uốn. 

 Định nghĩa : Điểm U (\(x_0;f\left(x_0\right)\)) được gọi là điểm uốn của đồ thị hàm số \(y=f\left(x\right)\) nếu tồn tại một khoảng (a; b) chứa điểm \(x_0\) sao cho trên một trong hai khoảng (\(a;x_0\)) và (\(x_0;b\)) tiếp tuyến của đồ thị tại điểm U nằm phía trên đồ thị còn trên khoảng kia tiếp tuyến nằm phía dưới đồ thị.

Mệnh đề  (Cách tìm điểm uốn): Nếu hàm số \(y=f\left(x\right)\) có đạo hàm cấp hai trên một khoảng chứa \(x_0\), \(f"\left(x_0\right)\) và \(f"\left(x\right)\) đổi dấu khi qua điểm \(x_0\) thì U (\(x_0;f\left(x_0\right)\)) là một điểm uốn của đồ thị hàm số \(y=f\left(x\right)\).

II. Các Dạng Đồ Thị Khảo Sát

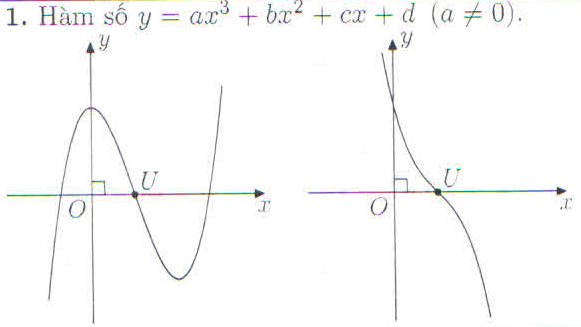
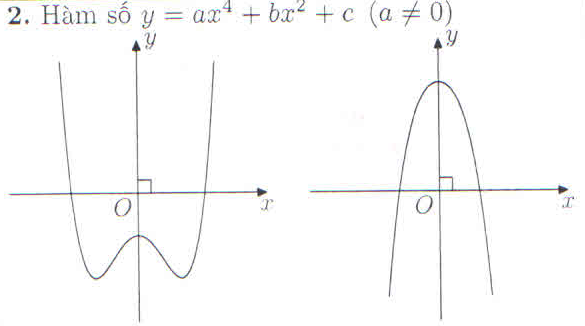
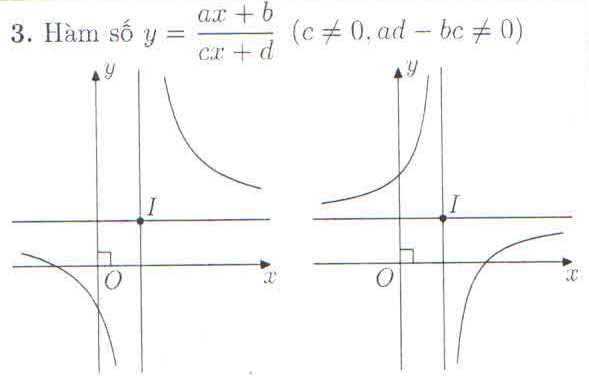
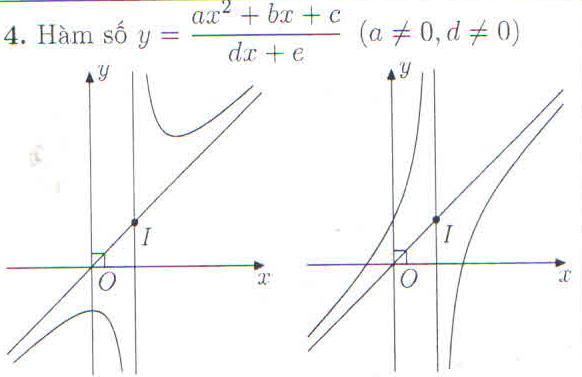
III. Ví dụ minh họa 

Ví dụ 1 : Cho hàm số \(y=x^3+3x^2-4\)

a. Khảo sát sự biến thiên và vẽ đồ thị  hàm số 

b. Biện luận theo tham số m số nghiệm của phương trình \(\left(x+2\right)^2=\frac{m}{\left|x-1\right|}\)

Bài giải :

a. Tập xác định : D = R

Sự biến thiên :

* Chiều biến thiên : Ta có \(y'=3x^2+6x\)

                                        \(y'=0\Leftrightarrow\left[\begin{array}{nghiempt}x=0\\x=-2\end{array}\right.\)

                                        \(y'< 0\Leftrightarrow-2< x< 0\)

                                 và  \(y'>0\Leftrightarrow\left[\begin{array}{nghiempt}x< -2\\x>0\end{array}\right.\)

Suy ra hàm số đồng biên trên mỗi khoảng \(\left(-\infty;-2\right)\) và \(\left(0;+\infty\right)\); Hàm nghịch biến trên \(\left(-2;0\right)\)

* Cực trị : Hàm số đạt cực đại tại \(x=-2,y_{CD}=0\)

                                đạt cực tiểu tại \(x=0,y_{CT}=-4\)

* Giới hạn : \(\lim\limits_{x\rightarrow+\infty}y=+\infty;\lim\limits_{x\rightarrow-\infty}y=-\infty\)

* Bảng biến thiên : 

* Đồ thị : Đồ thị (C) của hàm số cắt trục hoành tại A(1;0)

b. Ta có \(\left(x+2\right)^2=\frac{m}{\left|x-\right|}\Leftrightarrow\left|x-1\right|\left(x^2+4x+4\right)=m,x\ne1\)

Xét hàm số  \(f\left(x\right)=\left|x-1\right|\left(x^2+4x+4\right)=\begin{cases}x^3+3x^2-4;x>1\\-\left(x^3+3x^2-4\right);x< 1\end{cases}\)

Suy ra đồ thị hàm số \(y=f\left(x\right)\) gồm phần đồ thị  (C) với x > 1 và đối xứng phần đồ thị (C) với x < 1 qua Ox

Dựa  vào đồ thị suy ra :

* m < 0 phương trình vô nghiệm

* m = 0 phương trình có 1 nghiệm

* 0 < m < 4 phương trình có 4 nghiệm

* m = 4 phương trình có 3 nghiệm

* m > 4 phương trình có 2 nghiệm 

Ví dụ 2 : Cho hàm số \(y=x^4-2x^2-1\)

a. Khảo sát sự biến thiên và vẽ đồ thị (C)

b. Tìm m để phương trình \(\left|x^4-2x^2-1\right|=2m\) có 6 nghiệm phân biệt

Bài giải :

a. Tập xác định : D = R

Ta có \(y'=4x\left(x^2-1\right)\Rightarrow y'=0\Leftrightarrow\left[\begin{array}{nghiempt}x=0\Rightarrow y=-1\\x=\pm1\Rightarrow y=-2\end{array}\right.\)

Giới hạn : \(\lim\limits_{x\rightarrow\pm\infty}y=+\infty\)

Bảng biến thiên 

Hàm đồng biến trên \(\left(-1;0\right)\) và \(\left(1;+\infty\right)\); nghịch biến trên \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)

Hàm số đạt cực đại tại \(x=0;y_{CD}=-1\)

Hàm số đạt cực tiểu tại \(x=\pm1;y_{ct}=-2\)

Đồ thị :

Do hàm số \(y=x^{ }-2x^2-1\) là hàm số chẵn nên (C) nhận Oy làm trục đối xứng 

b. Số nghiệm của phương trình đã cho là số giao điểm của 2 đồ thị \(\begin{cases}\left(C'\right):y=\left|x^4-2x^2-1\right|\\\Delta:y=2m;\Delta\backslash\backslash Ox\end{cases}\)

Ta có đồ thị : 

Dựa vào (C'), suy ra phương trình đã cho có  6 nghiệm phân biệt khi và chỉ khi :

\(1< 2m< 2\Leftrightarrow\frac{1}{2}< m< 1\)

Ví dụ 3 : Cho hàm số \(y=\frac{-x+1}{x-2}\)

a. Khảo sát sự biến thiên và vẽ đồ thị hàm số

b. Biện luận theo m số nghiệm của phương trình \(\left|\left|x\right|-1\right|=m\left|\left|x\right|-2\right|\)

Bài giải :

a. Tập xác định : \(D=R\backslash\left\{2\right\}\)

Sự biến thiên :

* Chiều biến thiên : Ta có \(y'=\frac{1}{\left(x-2\right)^2}>0;x\ne2\) suy ra hàm số  đồng biến trên các khoảng \(\left(-\infty;2\right)\) và \(\left(2;+\infty\right)\)

* Giới hạn : \(\lim\limits_{x\rightarrow+\infty}y=\lim\limits_{x\rightarrow+\infty}\frac{-x+1}{x-2}=-1\) 

               và \(\lim\limits_{x\rightarrow-\infty}y=\lim\limits_{x\rightarrow-\infty}\frac{-x+1}{x-2}=-1\)

                      \(\lim\limits_{x\rightarrow2^-}y=\lim\limits_{x\rightarrow2^-}\frac{-x+1}{x-2}=+\infty\)

               và \(\lim\limits_{x\rightarrow2^+}y=\lim\limits_{x\rightarrow2^+}\frac{-x+1}{x-2}=-\infty\)

* Tiệm cận : Đồ thị có đường tiệm cận ngang là \(y=-1\); đường tiệm cận đứng là \(x=2\)

* Bảng biến thiên :

* Đồ thị :

Đồ thị hàm số cắt trục hoành tại (0;1); cắt trục tung tại \(\left(0;-\frac{1}{2}\right)\) và nhận giao điểm I(2;-1) của hai tiệm cận làm tâm đối xứng 

b. Ta có \(x=\pm2\) không là nghiệm của phương trình nên : 

                \(\left|\left|x\right|-1\right|=m\left|\left|x\right|-2\right|\Leftrightarrow m=\frac{\left|1-\left|x\right|\right|}{\left|\left|x\right|-1\right|}\)

Xét hàm số \(\frac{\left|1-\left|x\right|\right|}{\left|\left|x\right|-1\right|}=y\) có đồ thị (C)

Khi đó đồ thị \(\left(C_1\right)\) gồm :

- Phần bên trên trục hoành và bên phải trục tung của đồ thị (C)

- Phần ở phía dưới trục hoành, bên phải trục tung của đồ thị (C) lấy đối xứng qua trục hoành

- Phần bên trên trục hoành và bên trái trục tung của đồ thị (C)

- Phần ở phía dưới trục hoành, bên trái trục tung của đồ thị (C) lấy đối xứng qua trục hoành

Từ đồ thị ta có 

* Với \(0< m< \frac{1}{2}\) và \(m>\frac{1}{2}\) thì phương trình có 4 nghiệm riêng biệt

* Với m = 0 thì phương trình có 2 nghiệm phân biệt

* Với \(m=\frac{1}{2}\) thì phương trình  có 3 nghiệm phân biệt

* Với m < 0 thì phương trình vô nghiệm