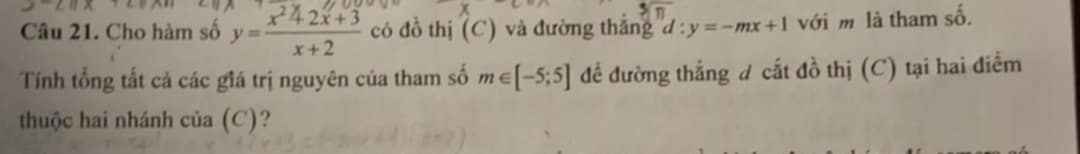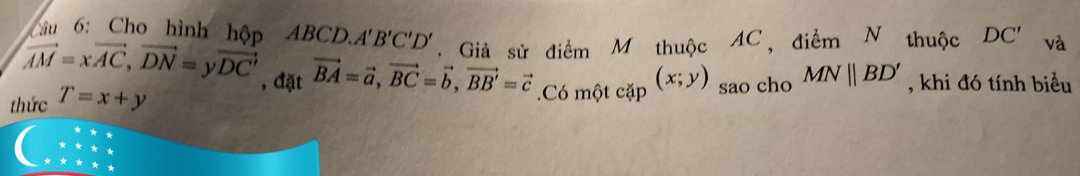Che bài sao giải 3    -.- 

\(\overrightarrow{MN}=\overrightarrow{AN}-\overrightarrow{AM}=\overrightarrow{AD}+\overrightarrow{DN}-\overrightarrow{AM}=\overrightarrow{BC}+y\overrightarrow{DC'}-x\overrightarrow{AC}\)

\(\Rightarrow\overrightarrow{MN}=\overrightarrow{BC}+y\left(\overrightarrow{DC}+\overrightarrow{CC'}\right)-x\left(\overrightarrow{AB}+\overrightarrow{BC}\right)\)

\(\Rightarrow\overrightarrow{MN}=\overrightarrow{b}+y\left(\overrightarrow{c}-\overrightarrow{a}\right)-x\left(\overrightarrow{b}-\overrightarrow{a}\right)\)

\(\Rightarrow\overrightarrow{MN}=\left(x-y\right)\overrightarrow{a}+\left(1-x\right)\overrightarrow{b}+y\overrightarrow{c}\)

\(\overrightarrow{BD'}=\overrightarrow{BA}+\overrightarrow{AD'}=\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{DD'}=\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\)

\(\overrightarrow{MN}//\overrightarrow{BD'}\Leftrightarrow\dfrac{x-y}{1}=\dfrac{1-x}{1}=\dfrac{y}{1}=\dfrac{x-y+1-x+y}{1+1+1}=\dfrac{1}{3}\)

\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\)

\(\Rightarrow T=x+y=\dfrac{2}{3}+\dfrac{1}{3}=1\)

Lĩnh vực công nghệ \(n_1=20,\) số liệu chia theo khoảng lợi nhuận

Lĩnh vực thực phẩm \(n_2=20,\) số liệu chia theo khoảng lợi nhuận

Giá trị trung bình: \(\overline{X}=\dfrac{\sum f_i.x_i}{n}\)

\(f_i:\) là tần số

\(x_i:\) là trung điểm khoảng lợi nhuận

\(n:\) là tổng số người đầu tư \(\left(n=20\right)\)

Phương sai: \(\sigma^2=\dfrac{\sum f_i.\left(x_i-\overline{X}\right)^2}{n}\)

Độ lệch chuẩn: \(\sigma=\sqrt{\sigma^2}\)

Sau khi lập bảng tính \(x_i;f_i.x_i;f_i.\left(x_i-\overline{X}\right)^2\) cho mỗi lĩnh vực công nghệ và thực phẩm ta được :

\(\overline{X_{công.nghệ}}=0,85\)

\(\overline{X_{thực.phẩm}}=0,75\)

\(\sigma^2_{công.nghệ}=1,3275\Rightarrow x=\sigma_{công.nghệ}\approx1,15\)

\(\sigma^2_{thực.phẩm}=0,9875\Rightarrow y=\sigma_{thực.phẩm}\approx0,99\)

\(\Rightarrow x-y=1,15-0,99=0,16\)

\(g'\left(t\right)=\dfrac{-t^2-2t+8}{\left(t+1\right)^2}\)

\(g'\left(t\right)=0\Leftrightarrow-t^2-2t+8=0\Leftrightarrow\left[{}\begin{matrix}t=-4\\t=2\end{matrix}\right.\)

Lập BBT ta thấy \(g\left(t\right)\) tăng trên \(-4< t< 2\) và giảm trên \(t< -4\cup t>2\)

\(\Rightarrow g\left(t\right)_{max}\) tại \(t=2\)

\(\Rightarrow\) Nồng độ thuốc trong máu của bệnh nhân cao nhất sau \(2\left(giờ\right)\)