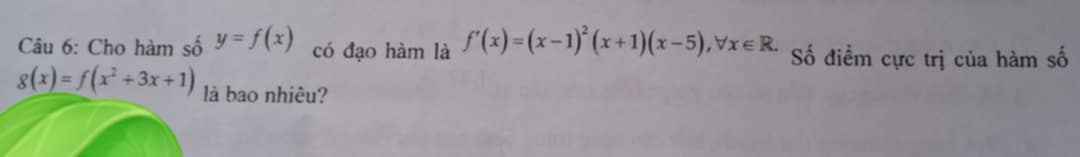
| https://tuyensinhyduoc24h.vn/tin-tuc/dieu-duong-la-gi- |
Đúng 0
Bình luận (0)
a) Đúng
b) \(f\left(x\right)\) nghịch biến trên \(\left(1;+\infty\right)\Rightarrow f\left(x\right)\) nghịch biến trên \(\left[4;10\right]\Rightarrow\max\limits_{x\in\left[4;10\right]}=f\left(4\right)\)
\(\Rightarrow\) Sai
c) \(TCĐ:x=1\Rightarrow x-1=x+b\Rightarrow b=-1\)
\(TCN:y=2\Rightarrow\lim\limits_{x\rightarrow\infty}f\left(x\right)=\lim\limits_{x\rightarrow\infty}\dfrac{ax+1}{x-1}=2\Rightarrow a=2\)
\(\Leftrightarrow a+b=2-1=1\)
\(\Rightarrow\) Sai
d) \(y=\dfrac{2x-1}{x-1}\left(C\right);y=-x+m\left(d\right)\)
Phương trình hoành độ giao điểm của \(\left(C\right)\&\left(d\right):\)
\(\dfrac{2x-1}{x-1}=-x+m\)
\(\Leftrightarrow2x-1=-x^2+mx+x-m\left(x\ne1\right)\)
\(\Leftrightarrow x^2-\left(m-1\right)x+m-1=0\left(1\right)\)
\(\left(C\right)\cap\left(d\right)\) tại 2 điểm phân biệt \(A;B\) \(\Leftrightarrow\)\(\left(1\right)\) có \(2\) nghiệm phân biệt \(x_A;x_B\) khi và chỉ khi
\(\Leftrightarrow\Delta=\left(m-1\right)^2-4\left(m-1\right)=\left(m-1\right)\left(m-5\right)>0\)
\(\Leftrightarrow m< 1\cup m>5\left(2\right)\)
Khi đó \(x_B-x_A=\dfrac{\sqrt{\Delta}}{a}=\dfrac{\sqrt{\left(m-1\right)\left(m-5\right)}}{1}=\sqrt{m^2-6m+5}\)
\(y_B-y_A=-x_B+m+x_A-m=x_A-x_B=\sqrt{\Delta}=\sqrt{m^2-6m+6}\)
\(AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}=\sqrt{10}\)
\(\Leftrightarrow\sqrt{\Delta+\Delta}=\sqrt{10}\)
\(\Leftrightarrow2\Delta=10\)
\(\Leftrightarrow m^2-6m+5=5\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=6\end{matrix}\right.\) thỏa mãn \(\left(2\right)\)
\(\Rightarrow\) Có \(\left(2\right)\) giá trị \(m\) thỏa mãn đề bài
\(\Rightarrow\) Đúng
Đúng 1
Bình luận (0)
\(y=0\Leftrightarrow\left[{}\begin{matrix}x=1\\g\left(x\right)=x^2+2mx+1=0\end{matrix}\right.\) có \(3\) nghiệm phân biệt ( \(2\) điểm cực trị nằm khác phía với trục hoành)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'_g=0\\g\left(1\right)\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-1>0\\2m+2\ne0\end{matrix}\right.\)
\(\Leftrightarrow m< -1\cup m>1\)
mà \(m\in\left[-16;16\right]\)
\(\Rightarrow m\in[-16;-1)\cup m\in(1;16]\)
\(\Rightarrow m\in\left\{-16;-15;...-2;2;3;...16\right\}\) \(\left(m\in Z\right)\)
\(\Rightarrow\) Tổng số giá trị \(m\) là \(2\left(16-2+1\right)=30\)
Đúng 2
Bình luận (0)
a) \(f'\left(x\right)=\dfrac{-2}{\left(x+1\right)^2}< 0,\forall x\ne-1\)
\(\Rightarrow f\left(x\right)\) nghịch biến trên \(D=R\backslash\left\{-1\right\}\)
\(\Rightarrow\) Sai
b) \(f\left(x\right)\) nghịch biến trên \(\left[1;2\right]\)
\(\Rightarrow f\left(x\right)_{min}=f\left(2\right)=\dfrac{2.2+4}{2+1}=\dfrac{8}{3}\)
\(\Rightarrow\) Sai
c) \(\lim\limits_{x\rightarrow-1}f\left(x\right)=\infty\Rightarrow TCĐ:x=-1\)
\(\lim\limits_{x\rightarrow\infty}f\left(x\right)=2\Rightarrow TCN:y=2\)
\(\Rightarrow\) Đúng
d) Phương trình hoành độ giao điểm của \(\left(C\right)\&\left(d\right):\)
\(\dfrac{2x+4}{x+1}=2x+m\)
\(\Leftrightarrow2x+4=2x^2+2x+mx+m\left(x\ne-1\right)\)
\(\Leftrightarrow2x^2+mx+m-4=0\left(1\right)\)
\(\Delta=m^2-8\left(m-4\right)=m^2-8m+32=\left(m-4\right)^2+16>0,\forall m\in R\)
\(\Rightarrow\left(1\right)\) có 2 nghiệm phân biệt
\(\Rightarrow\left(C\right)\cap\left(d\right)\) tại 2 điểm phân biệt \(A;B,\forall m\in R\)
\(\Rightarrow\) Đúng
Đúng 1
Bình luận (0)